I think I’ve cracked the thing, finally.
Suppose we have a random array arr of 64 bit integers of n values (i.e. arr.size is n). We know that its size in bytes will be 8*n.
Firstly, we have to see how many chunks of 2**15 bytes there are inside arr. The total number of chunks will be equal to this number plus 1. Note that a more general way to get the total memory in bytes of the array using numpy arrays in python is arr.nbytes (which in this example is equal to 8*n). Therefore the number of chunks m is:
m = arr.nbytes//2**15 + 1
where // represents integer division.
Now we need to know the size in bytes of the last chunk. But in python this may be obtained indirectly, as follows.
Each of the first m-1 chunks will have 2**15/8=4096 elements, since we know that they must have a byte size of 2**15 and hold int64 elements. Therefore, each of the first m-1 chunks are known to be arr[0:4096], arr[4096:2*4096], …, arr[(m-2)*4096:(m-1)*4096]. Finally, the last chunk will be arr[(m-1)*4096::], whose size is size_last_chunk = arr[(m-1)*4096::].nbytes.
Now we need to apply the compression, which in this case is zlib, and get the size of the byte arrays of each compressed chunk. With this information we can finally write the header_array, base64 encode it, concatenate the base64 encodings of this array and of all the compressed chunks, and finally write the XML file.
As an example, if we have m=4 chunks of a 16000 random int64 array, then we could do:
import numpy as np
import zlib
from base64 import b64encode
# making a random int64 array here for the example
rng = np.random.default_rng(seed=0) # random number generator
arr = rng.integers(low=0, high=3, size=4096*3+3712, dtype='int64')
# this array was chosen to have 16000 elements, equal to 3 chunks of
# 4096 elements plus one chunk of 3712. This can be plotted in a vti
# array of extent 32, 25 and 20
# number of chunks
m = arr.nbytes//2**15 + 1 # equal to 4 here
# compressed chunk 0
compr_chunk0 = zlib.compress(arr[0:4096])
# compressed chunk 1
compr_chunk1 = zlib.compress(arr[4096:2*4096])
# compressed chunk 2
compr_chunk2 = zlib.compress(arr[2*4096:3*4096])
# compressed chunk 3
size_last_chunk = arr[3*4096::].nbytes
compr_chunk3 = zlib.compress(arr[3*4096::])
# header array, assuming uint32 headers in the XML file
head_arr = np.array([m, 2**15, size_last_chunk,
len(compr_chunk0), len(compr_chunk1),
len(compr_chunk2), len(compr_chunk3)], dtype='int32')
# base64 encoding of the header array
b64_head_arr = b64encode(head_arr.tobytes())
# base64 encoding of the concatenation of the compressed chunks
b64_arr = b64encode(compr_chunk0 + compr_chunk1 + compr_chunk2 + compr_chunk3)
# print to XML file (or to sys.stdout, in this case)
print((b64_head_arr + b64_rest).decode('utf-8'))
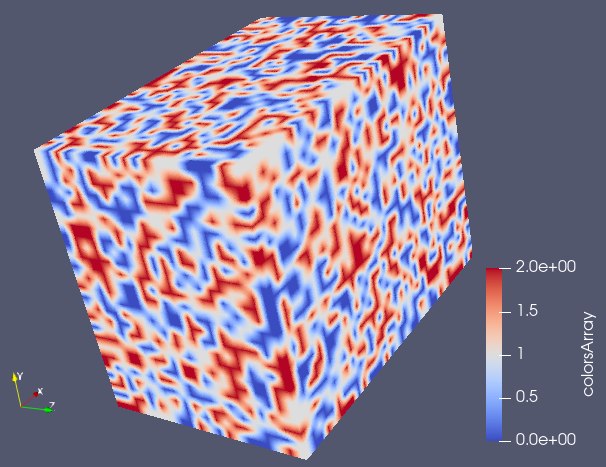
We can then write the .vti file found at the end of this post considering a 32x25x20 mesh and obtain the following figure. The binary CellData was generated using the above python code.
<VTKFile type="ImageData" version="1.0" byte_order="LittleEndian" header_type="UInt32" compressor="vtkZLibDataCompressor">
<ImageData WholeExtent="0 32 0 25 0 20" Origin="0 0 0" Spacing="0.05 0.05 0.05" Direction="1 0 0 0 1 0 0 0 1">
<Piece Extent="0 32 0 25 0 20">
<PointData>
</PointData>
<CellData Scalars="colorsArray">
<DataArray type="Int64" Name="colorsArray" format="binary" RangeMin="0" RangeMax="2">
BAAAAACAAAAAdAAAAQcAAAEHAAAFBwAAWgYAAA==eJy1l8EOJDkIQ2vn/z96Dqu+WLLeM1XDpZUUAULAuP88/8t/8bvKnzif69xv31Mv7ed+89fO5fnUS7spLV6Sdt+0a/PW8k377XuLw8bdzj2xbvotj7ZO2ruTvZRml+xZfy1Oeq/U/4ntm1Wf/JNd8rf2/7Vf3tY5vVuLr+WR6mU9b/GMcOCJNeG5xcu3dUT5f1uf63ukPTpPOGXnAfknuerZOrjiwTq/yG5b27lE+mu8TYg32Hq1fm39XXF85VUWT2y9kNBcXOt87QMbj43rOvfonin2fZq+jTfja/ZsXa74THFlfJY/NVnxc+VpaYeE6prskN6KA1f8XOtu7c+Vz9pzT/me++s8yPNtvfIpy0evdb7ywBW/LF9r+ha38ru95/qeKw5ZPE5/b3ke2cv4cm3/nzS/zZ7tK4rngf32nXBkzVfbtzxl5Vt2/lgcyH3b5/Z/wco7Um+tr+t8tfe98vPruZQVr/Lcyg+aXOvD8m/qR8KjtNvkOheaneu8I95t80Z8weJ7yjUO+36U3yvfWeeKzaflp5bPvMXVZj/F8rxc27ljcTL11/m85sne48o3r33V/FOf5bmVx9u6s/lbeUl+p/ekPl55VgrZtfXZZOXR9vsVP3Jt+fxX8Vv+QrxtnV+5tnxpnWu5tnVK5yg/FtfXfljtNnuWr1mecY1j7du2Jrt2DpL/Ky+h+k55e474kc3Hdf3VvW19rH2x8huLrxSX7acVl3NteTLZtedTWl6u/Mbi94pjK46vdWv/36T/FFsvb+uw+aN3Wvl883ONZ53f+Z30r/1h+/Ut33xAb+U9+d3Wj70H2bdzY8W3NR+2rnL/6u8nVz7Zzq/4SvZtXa73o+8Wt2yf0Pn23eJ7+rPxkZ6d++uctvXc/K48x+LkiuNXHH3LO6iuCa8pL2ve2v46H6hem37z1+LKfTvnV/5h46F3fIvr1J8p1znX5Mpv7PuvvNTiUMZp++I6p+y7kb2m9zVvX3HliqdNv8V1xcdmj+rn2mfk74n1Wj+EJ83+yttWnLD3W3lYysr78lyzs+bZnqN3vPJCercWN9m3ebL2rH1rh+JecfEnhG+2vu272XpY64XiWnkNvUezT7/Nvp2Tbd/ygpXXUt00ofq197dzdsUJy0NtXqju1nlP+yt/o/q68hmLdyk2Hjuvv9Ij3Et98rPyDcu7LC/N/be80vITy2eafM3DVjxf4yQhvtv2LR5aHmHjsXhH8TV/X/HUFWftPajen/Ld1t3KD5pQnpr+lRc/8N3GQfqWT7b1mv8U6p/0Y/ntlc+sdb3Os/X8yvNTbH2svKfpNb9XfCV9278tLuJfNn8pFi+u/D3Pr/PJ5sHOJVuntp5SyP7Kq1a8s37auRZH6l/n7poXW0eWh652rrzn6/pPoe8pNl8WH62dK76Q/+avrX9i35t4WLObdiwfXOesjectX7Z1bufcNf7ctzyV6m7FL1sXdp6RvMXfr3i5nUNv587K4yyftPhq+259X9snV56dYuva8jWbR5unFi+dT31b701WvKW82HPEt9Z3SjuEYxSXxdXV73X+ZLxN7Du0uKx+82vjXfF5rcP1PazdFNuvzX6TK6+m89bOWu/rfLR9Z9+R5tDaNytPpXhI/hWeWh654vM6p9f5aN+T7p37K3+g+Nd8PXKdQu9Dc+rKv+gdrrxlxdN2nvAx9+27fNXXNn9PWdN7Ul/Y/OT3te+a/dWfxWs6T3j0dq6kf/seaXfFTeuP7tP2bV+v85H60uLfOh/ST/Nv41j/l6x8uOlRna/5eMt31nmSfiyPsH2Z+4QD9N36szzb4ln6e3t/y9MsXyC8bHbbd8uLLN+x9Uf2LS7bPrzmmYR4xFrfNh57/+Yn48zvFh9aPJZnrfzjiotXPtLiXvve4vbKw+z7X+ey5VvtO9lfz/1kxSkSG2fuX/m11X9iTfVjcYjs5neLK2/nCvWbrT/KB8Vr8SXlX/MU+842vtWfrWfLv691sPLglCsurXPO9v3a3/R+dr60c3aeWb678pkUqpOV/6xz3fJ9skf3S1lxmfpg7T9bPxYnbV1RvFRXX+HJOifovi2O1L/O3RU/LN+1vyv/Wu9p+4z827lDfHzlV2TvLQ6kfrNj+z7Fzo/mb+Upzb6tVzs3bR5snpu8za+dw3TO4luKzaOtb4uX6/yje6R/W8/rPFrnohU7B+29rH3SX/lxi8f2teXXP7E8p8XRxNbd+u4r38hzKw+0+E35t7j+dv43uymWr5Bd+z+h6Vv8fssrLP9u8nUfWx69xrvy0yY2L5bHp11aX+s+/dNctnNo1cs42pr0rnPN5ifF8pimT3OK/K11Svi/zsVrHVzn+IorhJep1+J5y3/XPrX83PbbU/avcyj1/xV/Sr22tvt/Aes3ECB4nK2XS7LsOg4D6/b+F/1GZ4JoRCYoc1JhW6IofgDUv9//t//Fb9q/si5//8Vv7m/W1uevja/5ae8zflrXzv8zykvL53qPFvcaRzu37afzWzx0b4rH5rmtb+ektTpTXdr9Wjzkh+LMuOw8tjqvfWT32f5t9Wr1yHVUf5uftt7GS/ew369zSfdu/dn69YpT6zw2/+u5K0+k2TrY+zX/az+krfN9PZ/wcJ3z5qetpzlYcd7icq6380LntfWvc0U40ozm7Oqv+V91Q/qxc/71PWgO6dnqsJWXXueO5p3m3/Yn6Uh7LuWH6t7Opf4iXfdV31N/W79U/1xHZvXtWreVz22+iEfo+4qnts4rntv5tLy/zruNh/rP5n/VcRaX2/62/qqv02w/WT2R39d5pHlp57TnZpZnc73FZcr7mh+rgwkPVj+vc7rqdbue5jDXtfPW/re4ks82Xot31zqv+vw6tys+Eu+s+uyKo1YHkF3zbetGcVE9LT+t/XfFPatT17xavdPiTCN8pPo2P/k+n1f9Z/nb4g3Fl88Wz1/x/qrDbRwrDn1Vp9c6NLP9a/k6932NAxav1nvl+3Wd1Unt2eL5mqdmV7yy+Gxxr5nV41Yf2L5Jszyz6i/bd7b/aB/NncUT23eWR6966KpDWjyEa6tOobiaf8KVVadYHrBzuuLCtY/pO/Hl1zy96se2z/Yt+bVzbvHZ4laLi/xY3Wv7KPc3o/66zrGtg9UNlk/z/YpHzcjfyk+5rj2/4t+q/ywPvsaz4kOaxZtVb1kdl3E0u+qr61zYeqdZ3UH78v3VD+nuK2++6ozmz+KSvcdVH1jdbPl27Re6d/Nj4/rF91cdY++/nveVLrO8Rzh+zddajzR7Xvu+6pxXfULxtLyueqKds36/6uXcb/Ua5WvVV1Rny69WT6y67Gt8Jd62OoH6tb1f+6UZ8dG1r9Jo3lb90fzk+5VvV71CebB8Zf+X0H2o31deas9pr3x0vU+ut/9XLH5aHLP4leflurUvKM/5vPZHs6/zS/y76j6r/2x9bPwt3ozP6pG2r63L95aX1r644tWK04QXKx9ZHLV4t+Y/v69zQPHQ/Frd92e239OsvmpxveIvrVvrZvfZvrrOx6oDXnUQ9ZPVMxZfXvlhNat7c73Ni+2bNJqXfH+t41W3UB+v851m6/m1vrrqTFvv9GPxOuNZ9QX1k+Vli6t0rtXpFl9sn7f9tv9tn6et+ct9Vn+tOHnlEav7v37fjOK397C26iDrn3hvxfOvdJvlZcsLlh/s3Nr5ovd2Dlo8lkeu+n7VmeSHeMzy+698t/1I+f3Fuvad3qcfi+f2/0J7f9XD6xxf/f/G56/udcVje94vvtt409Z+SXvFP3u/5i/3rXOW6175e9Wj7fx1Dqhv1/8vFucsH6y8t+pNy5vtve2nXE/xr7izxnHtE+LZ9mzrZPXRaraPqB/WOqTZ+Wrr17zZ/0WrjrL8kM8rf9N9bbyrviQ/Nj8Wj151JOn0lZdpHcVF/iyvtDgs713xlPxYXd/8Wp1v54PmpJmNz/YZ8dqV59d4yf+qf0gfWn2w9oOtq8UfG7fVDdSnVz/5/ivcu/I8+bd5Tj9XozykWb1H7y3+2fm0utX+b6Dz6VyLC2vc7Vzan/usnrE63fq3PGL/N6y68wffbfyv/U7nWr2Yfloc13pd54X6+tqnK9/Z51WvUTzUPxZ3r+c2o+9tneWnFo/9H0H1sn1GfvN7W09zdMVTmss/s3Vo56SfFQdsnsn/NT47T1Rfi+/EJ+v/Aoon3+cz9aGtT74nf9d99r4rPq76MP1Z3rC65Tov9HvVA5SHNMrjqi+venW113ytOG771+ICzRf164pL7dnmrZ1PRuvXOWj7Ka8UX9rKP82v1aukc5rfX6xbdRXts/Ntcf/aj3T+Ky+kvepUq08sXl/1x2v+Vpx85VOKp5nNu8WLK6/Z/qd6tnPSL60jPLX5+aou6/8CivNVf6zz+Iqjax/ReavubOekWTxv/i0/ptn8ph87D22frXPzk2bzb/dRP1zjWXVH82vjojlY75txkL+23tbX8sZrf1/x/KrHrvXK5xWvSDe18ywOpBHOEy5a3GzPq65q8bVz7Zzac61usfpqnWPLr83PytN/9pWusPOaZvNKOGbrlOub2fqTP8vvNk9Wd1HchHvt3LWOV/4m3mxm9W3zt+o+269rvik+e85r39A8WX2x8r7l13ZO+mtx2PMtvpLOsX6s7rB9kLbGnX7Jzyturjp2xZ1VZ6z62PKTxWerA671sLoo3//i+6pXqS8I75tdeWjVHSsOWt5Y593qOxu/1QtrXvM79bWdk3bOitN57lWXEr/l85VPLV+381e8zn3rPNh8r3O63nPVM1Rn6u/1/nRO7v8PbF8P5XictZhBDiM5DAMz8/9HzymHJUBUUc7qErTblmVZItn5+/mv/ZG/f2Pd3/j983GWftJyv/Sb4/Y5923x5jjlob1v+9v8rvGveaK46X2ava8cb36atTg/8Zx5u65r83MdWbuPfJ/PbZzure3/Ot6M8KNZu6f2S/HZcbqHax+s8bT91vPafBOutHF6v95fi5fya3Er/TX/6/4tnly/8pDNO8VxvVfik+bnymvNb3u+8gfVYZuX42t+7X2REZ/R/us86of1Hmw8tm+brThIRnm3/E3PrV/WPksjXGpxtfhoPsX1ikfXum5+Lb61dYQLlkeueV55ZNUH6/P6/UVx5rx27ly37kd9uH4nUlzX75NPmUf7tHVrvVgcpHjpHm0f2fu68ueqM5sfqiOLf2181W20L82338n2ntd4rvrNzqd8Wly1fU/jbR/b52vfrvfWbP0fgIx4YM1b80/Pv7pHqiOLP/b70+KizZPlY+IRm4+1/y1uW/1lz9vWr/lt/tfzt/hs3Vz7LO1ap1ecpn2aXXnM/uY+K15b3Glm8cXiDeEWrfvaVfet+LHef7NXvljXUxx0f5b/7TrL5xRXznvF61X/E24QDq55pX2ueuVrhAdXfdL2pfuy69v+a73a95Rnyp/Fl5VnLc+RPlp1Xdp6T6uutX18xYMWZ677Vb+u+cpxu4/FM8vXa3+86in7fq0nmm/r196r7aeWP6tzX/H2Ne8rz658Svlb8crWC5nVxza+5v9rtq5+pdPXOiQ8oDpL/81vW2fvwfbt6/2uurCto3uzfUi/FJ/V6Vfcy3HLLx94b89n47TPbf3ax81PzrP3n+9Jr9j9rL6yetbq1te+fdUxVq/RfJvnNMvTaz1c82P7M8fbcxrpr+Zn5Tsb71qvLU6bf4rD8knzY/kpn9d+o/2u/Ed8fOUvqrsr/lnddMW7NW6rh6/5tPfUbMW7tv61j1cdYPdfbeX1XGd5f9WXFA/Vy5pPi0MZVz5bHLM4c33f4sp5q56lurd1aO8/97F+LS/Z+ss4rudMszrY6kmK43p/K8/YvrE883/x1pXvr3ze9vmazR/hpPVn7/0aV/Ozjq99fdWRzW8a1QPlya7/lOf01+J67b8rn6/zVp2UtvIq3avVP7mu7Uc4kn6sTv2V/1XPtXjWfl392HOl31ddl0bna/MpDsKrlR+v+ba4RP288iP1mdVflt9tfbV1FsfyfT6vdfHr/l31ypo/wsdX/dD2afbKN2uf2V+Kb8XFq/5ptvLOFb/Srv3Q1ue+dP4VB9d4bN+0/VqcNO/6ns5rda/lhXxv80d+Le5R/zR/Vm/QvPRv8cryEdUp3e+veP6VXyiuFW+bn7S1z0kXkD6zdU+6su1veZb6gebTPVuezjhXvLc42vysOmI978oTa76bn7Q17zZv7b3l+TXvFqev/GTvd+WRfKZ7yPmkS5qfFR9XvviV7rM4Zvtx1a2rjqT9Sf+l33ymPJFetfVEeUkjvlp1IuV95d8rvzWz9WFxyO7T6qLt2/wRP179XfG77WfvecUje07qG3te2z9W36764hPjaeSH4rX4YuO7nqPF2czyqMW3VZ/ZvrP1dNVzKw+uevPKh1d9lX4s/q56NsdbPKuuoHpq+5D/VdevddxsPY/VKWmEo78yi79tPvV9W5fjaVZH03zbZ6+4TOvp/m0dr/rW6l+rxy1PrPlY9Yn9tbhv8aytz3GyK36SUX/k84pfax+veEV11+bZPF75jM6/6vm2zuqeXL/qeRvf+v2x4oO9tzZu+edrK9+0ebYeLW+lUT9edZ3VXcTz1+8Iq+fzPcVhcYN0OI3TvPae6ovqyv7muny256N8Uj2u3x8rjqxmddIVD1cdTPdF62xeLD9ez2HzResojvU7wPIe5XHFy4yDdJHFh/Rr8WI9n43D4muz9dxXHLS4S335GqfNf/Oz8k17//qd9KpnaZ/rvVK8K/4Rfqw8nkbz1v61ebU61N5jM4tvVt+3OGh+rmvxrXW36mvb5+mvzW/zLP/lfNtflo/te3v/1zq35ybcpHGrky3PXPXodXz9LqK6euVbu0+uIxxrcaw4+YpnVidYXrrii82z1euWl1e8u+qo5qfta+fZ/F15h3Dc6oAVbyzfWXyxuqkZrX/te8Jl8mfruPmzvEV9uca3jls9tvKTjXPtszTqc4t/ljdWnWJx3p4jzer7tQ6Jd9bn6zlX3WRxq9mqW679/YH3r/pv5WNbD1ZP2T6hOGz+2/rV/8qvaXRui9OU/9yvxWH1jtWHK0+0eGxd2H5/HSccWnFu1UM03+JPW/c1q4vzPdXHyhe2T2mczr3qAcu7ZFRnbX4+rzqC1hNvWPyxeaN9iT8/8N7y4MqHaVYPr3x05XPq+yuf2PqgfWwernX5ff4H8VcQJ3ictZdBjhwxDAM3+/9H5xDMhQBRRXmiy6DdsqyWJZLz+/PPfuH3D/w2+4X1P+CX7ykexcnnFj/Xm3+LZ7+r5ZX76LlZy5PWW12oH+h8qrM16rvr+RnX1qP527pSHalf7blU72s+q3+el35UZ4q34kY+23tf+9nGo33NWj4Z59qHV5zN/dQn+WznM22dj7ZvxSuae8snaz52fshovr7VrxmX9q/81fKiPAjXLL7YOtL5tI/Oa/FpPeMSvtj3FJfM3jfNleXLdv639BThi+XPXLf4vvIw1fFbfEXzSOdZ/F3xYsWZVYe1eK/1pz4jXLJ+qz6n72rxbX9lPOp/y+9WT+c+qp/Nx8Zfea/lQ/PT8rf+13Xbb+s8W3571dVWX1gczHwzLvmvcXN91Zsfs/oln63+J7P3Zvn/yh+vuiX9aC7TCNeoLs3/Y3a+ib+brbhMuizjWv5c60j1vM4h1W/Fs7Wu6zzb/w8fu+J07rd60eaR6/Ye1jpe8XLVxWtd6Vyr5y3e5nn53uqvNKufaH3Vfe18q3fS3/KD1S3kZ3HF5mvv1erClZ9Xnl3xhuZt7Seqc+Zj5zDPaedm/PZM82Pxef3fs+LNyk9W55C94nWaxVWLazQn69xQ/676+6rLWtz/1fdXnWvxx/Ke1ccWH6nudm5pDq59ZvvP6mN7fr5f9dTKv23/Ovd2PijuWt+1zy2urXhC+wgfM48rTtj8mq062tY749m5XnUM1TX9LM9T3Si/FUcyzxWX7P70a88Wx62esfOd/vaeLE9e80u/tj+fr/NN8S2/rjic7+1vi2Pvt+1P/1Vn2v617+nca74/sb7qDNuv356X9G/7Vzym86641s5f79nWfa2L7aN8f52n6/3YPrR6j+r1yvMUb8Xf1VY+JTym78x9H7NzT3FXvKW86PwVr678Z/Wy1V2WV9s5lJfln3UeVty0c/6Kh1cd/y19R/tXXU11s/sIn9PW+bjyEMV/xdWP2XuxfGL5lPpvxW3q35ZHGtXb5k3x13u1uH7V+VaPkJ/lk7WPr/1n67zyGvUZxV35zPb1qw60usTyHNmVZ61R/Wx96bmd+zFb/zSrYzKe5VdbH4sfaes8Eo5feSPPS7vqnVVPUF/Ye7L1XPlwnbMVB+39Zz7r3K541/xWPLX/W2zdbZ/luo2z/n+77rN6re2j77Q8RvPV1lc8bHnZfDOPa1+96od8n7bGtbx51dctXtrKf1TnPG/9/7H+/8l99nsyT8pv5a/ct+pIugfKi+7b1vHbOH6dL6tHm6063D63PGjOVxxvcVcd1M5P/9YHq85Io3uk/kuzOGPrQusZ96onrY5u5+W+lXfJVv5tzzbvV11h+9XiktXbtv8tr6Y/xbP4a3XDq55Pf8vDLa7lyzS7z/IczbvtQ/Jf+yrjfYzm9DovV56ydaf3FidW3l11LN3nqpPJ1jqv/2ss/1qefdWl7X3aFUfXPO13kF112op7VkdZnWLxajWb38qf6/+Fb/NK8191RtpV71g+onrZfZRve2/11SsuW56w/Ex6IePms8WjtZ9sHqt+o302j1X30jkZx+az8ufK/2m231d8oe+w32X12quuW/XIta4Z1+Zl+djyUprV7VZPWrxa5/sV7yz+rPe+6vzmd70n+91Wx7T9tL7OvcW7tr/lc/2u13mxuNTOW/UX5dPOaeuUT8vjlS9XvrN9YXXXqtcyvzWv9btzveWZZnVt+jejPrN80OJaHdr2UR70fSsfXfVQ+lGfrzqz5WPjrbhIfdH8Vz1B/Ez1a/FaXnS+vacVd9OPcIXmi/yoXte8bH2bf3tvcdfO3f/ixZXvW3653uK1PFbdROddedDqSTsfGb/Z+p7mv61f81h1iu3Lq85d9636yf4/sHy26gLLT5THygf2nDV/4r9v9dd1/sl/5V3bP2n23u25K7+R31q/FveK5xaHM95a15V3qL/ynDQ7h1ZfrDrcrlsczTzIrrhw1RuWL1d9kc+2ny0+W91m81rzTr9XHZlG9cj4V35teV7zpXOtnsnnK19ZPGp52P609SJcXnWQ5Tn7Pe3cVUc2v4xv91F91nuh71rnPPdbvbby/+t9Wn2U+9bftv9jVx1JcVe8uOZ57X/ivRXfLM59q29XPF3zXe85zfbNigOWhymP9XfFoTWexb9v8dtfRhoOXQ==
</DataArray>
</CellData>
</Piece>
</ImageData>
</VTKFile>