Hi all! We (@jaswantp @c.wetterer-nelson and me) have been working on a prototype to support discontinuous Galerkin (DG) finite elements (and hopefully many other novel function spaces such as mimetic techniques, X-FEM, CW-complexes, etc.). This post describes the problem and discusses a work-in-progress merge request with our prototype solution.
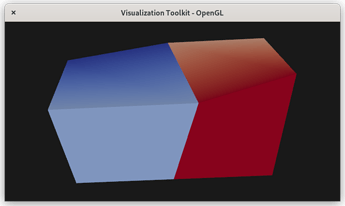
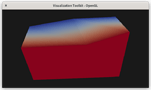
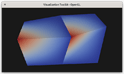
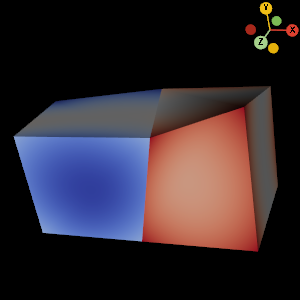
Figure 1. A screenshot of our prototype mapper rendering two DG hexahedra that share 4 corner points but still have field discontinuities along the shared boundary. This is achieved with a custom mapper that delegates most of the work to “render responders” for each cell type.
Problem Statement
As many of you are aware, vtkDataObject subclasses make increasingly-strong assumptions about the nature of data each can process. In particular, vtkDataSet is the first class in the inheritance hierarchy that introduces the notion of data with spatial extents. However, this is not the only assumption present. Below we outline some additional (and problematic for DG elements) assumptions.
Fixed set of cell shapes
vtkDataSet has a strict enumeration of cell types; external libraries cannot add support for new cell types to VTK’s set of types. This has led to a proliferation of cell types in VTK with some overlap between them.
We would like a data-object that accepts cells defined external to VTK.
1–1 relationship between arrays and fields
vtkDataSet adds vtkPointData and vtkCellData array containers and assumes that arrays in these containers have a 1-to-1 mapping to spatial functions (i.e., mathematical maps from locations in space to scalar, vector, or tensor values) which we will call attributes or fields. (Note that sometimes the arrays in the vtkFieldData instance inherited from vtkDataObject are treated as functions constant over all of space).
DG elements don’t fit the pattern of these two (three including vtkFieldData) specific array containers, which we’ll discuss next. However, even if DG elements could be adapted to the existing function types (which the vtkFiniteElementFieldDistributor does to some extent by duplicating points on shared boundaries), there are use cases where this correspondence between arrays and fields fails. If DG cells are expected to each have a different polynomial degree (for the same field), then multiple arrays are required (to specify the degree per element + per field and possibly additional connectivity entries). Also, there are other use cases (e.g., NURBS elements that have knot vectors in addition to values defined on control polygons), where we may wish to use multiple arrays to specify a single function in space.
Only two or three types of fields are supported
The assumption that arrays in vtkFieldData, vtkCellData, and vtkPointData array containers define
- spatially constant fields over all of space covered by cells;
- spatially-constant fields within each cell as determined by a single array value for each cell (cell-data); or
- spatially varying fields within each cell as determined by array values specified at “corner” points of cells (point-data)
respectively, does not match many finite element schemes. DG finite elements define fields that vary spatially within a cell but are not specified by values shared at boundaries (unlike vtkPointData arrays). Many codes use coefficients that are associated with edges or faces as opposed to cell corners. Some use generic degrees of freedom that are not associated with spatial locations or cell boundaries at all.
Field values must come from the same space as array values
Although not relevant to Lagrangian DG elements, some DG elements use function spaces such as H-curl. In these function spaces, the coefficients stored with each finite element are single (scalar) values, but the field evaluates to a vector or tensor value at each location in space. (The basis functions are vector/tensor-valued, so weighting them by scalars unique to each finite element produces a vector/tensor field using only scalar coefficients.)
We would like to specify the range of the spatial function separately from the array(s) used to defined the function.
Fixed set of visualization operations
Because vtkDataSet also provides an API to fetch cells into a uniform container (vtkCell and its subclasses), cells provide support for a basic set of visualization “operations” (isocontouring, cutting, clipping, evaluation, parameter location, boundary extraction). Other capabilities must be provided by filter algorithms that explicitly handle each cell type (or more frequently, complain when they encounter an unknown cell type).
We would like to separate the cell type from visualization operations that act on cells of that type.
Proposed solution
We are providing a prototype solution for comment that makes none of these assumptions. It provides a new subclass of vtkDataObject called vtkCellGrid. This subclass holds:
-
An arbitrary number of array containers rather than just two. Each container requires its arrays to have the same number of tuples but does not assume each container corresponds to a type of field.
-
vtkCellAttributeinstances that have a 1-to-1 correspondence with mathematical fields (or attributes or functions) and may reference any number of arrays from any number of containers above.One special
vtkCellAttributeinstance must be provided to map cell reference-coordinates into world coordinates; this is called the physical or shape attribute since it maps the cell into physical space. This field must provide vector values at each parametric coordinate. -
Subclasses of
vtkCellMetadata. Each subclass corresponds to a different type of cell (hexahedral DG cell, tetrahedral NURBS cell, etc.).
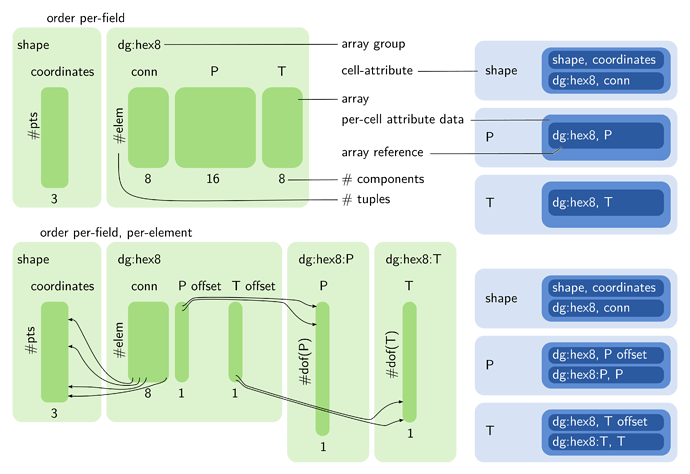
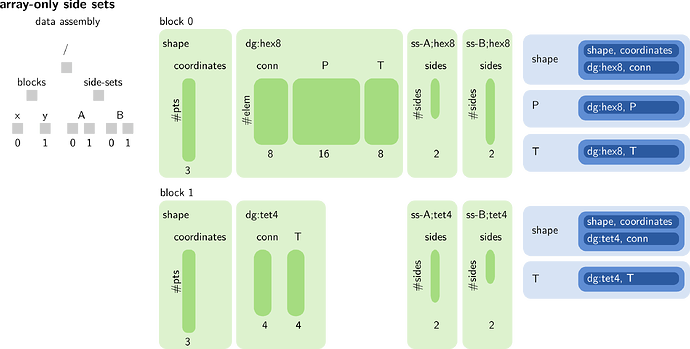
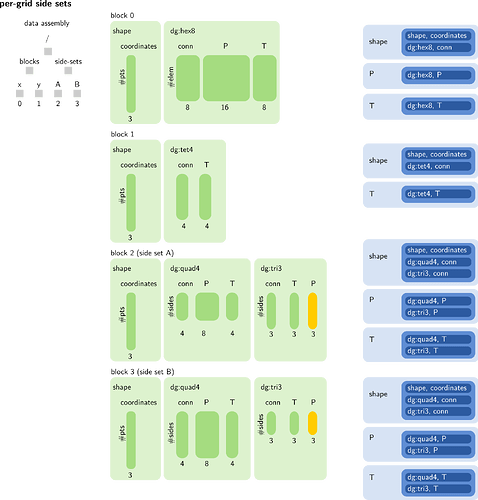
Figure 2. An example of how discontinuous Galerkin elements might be supported. The light green rectangles on the left are array containers that hold dark green arrays of matching size. The light blue rectangles on the right are
vtkCellAttribute instances corresponding to fields that reference arrays from the left. At top: the case where each field has the same interpolation order for all cells. At bottom: the case where each cell may have a different polynomial order.
Since one instance of any vtkCellMetadata-subclass is accepted, the vtkCellGrid can be extended by external libraries that add cells of new types. However, we also want external libraries to be able to extend VTK’s cell types by adding support for new visualization operations. To support this, we introduce vtkCellGridQuery, which is an object passed to a vtkCellGrid in order to perform an operation on (or obtain information about) cells of every type in the vtkCellGrid. External libraries then register instances of a vtkCellGridResponder that can respond to a particular query type for a particular cell type. For example:
vtkCellGrid* grid;
vtkNew<vtkCellGridBoundsQuery> boundsQuery;
if (grid->Query(boundsQuery))
{
vtkBoundingBox bbox(boundsQuery->GetBounds());
}
else
{
std::cerr << "Some cell type could not respond to this query.\n";
}
This way, a library that adds a new cell type can add responders for queries added by a different external library.
Prototype results
We have implemented the data-object classes described above plus the following in order to validate the approach:
vtkCellGridReader– a simple JSON-based reader that constructs instances ofvtkCellGridfor testing purposes.vtkCellGridBoundsQuery– A query to compute extents of all cells of all types in avtkCellGrid. A responder for discontinuous Galerkin cells is provided (not specific to any particular cell shape). The query is used byvtkCellGridinternally to compute bounds for the grid.vtkCellGridSidesQuery– A query to compute external sides (i.e., external faces of volumetric cells; external edges of surface cells) of cells in avtkCellGrid. A responder for discontinuous Galerkin cells is provided (not specific to any particular cell shape). A filter namedvtkCellGridExtractSurfaceuses this query to add an array of sides to an input cell-grid. The array is used by our prototype renderer below.vtkOpenGLCellGridRenderRequest– A query to render external faces of avtkCellGridto an OpenGL renderer. This query is used by a cusomvtkMappersubclass namedvtkOpenGLCellGridMapper. A responder for discontinuous Galerkin hexahedra (namedvtkDGHexahedronOpenGLRenderer) is provided.
You can try the prototype out by checking out VTK merge request 9499.
-
Build the branch of VTK from MR 9499.
-
Copy the included
test-prototype-dg-mapper.pyfile and test data (dgHex2d.dg) from the top of the source tree to your build tree. -
Run
./bin/vtkpython ./test-prototype-dg-mapper.py. Many debugging printouts are included. The following keys demonstrate different features of the prototype python demo:Key Action Ctrl+d Cycle through rendering L-1 and L-2 norms of parametric coordinates instead of coloring the hexahedra by field value. Ctrl+b Cycle through rendering of basis functions instead of coloring the hexahedra by field value. Ctrl+f Cycle through coloring the hexahedra by different example fields. One is continuous at the shared boundary, but 3 others are not. r Reset the camera as well as the color-by mode (to color by the currently-selected scalar field).
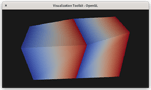
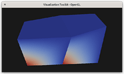
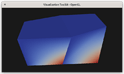
Figure 3. Cycling through parametric coordinates using the Ctrl+D key. The top row shows the r, s, and t coordinates, respectively. The bottom row shows the L-2 norm of the r+s coordinates and s+t coordinates, respectively (the t+r norm is solid red for the viewpoint in the screenshots).
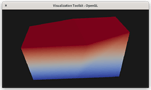
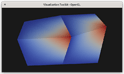
Figure 4. Cycling through 4 of the 8 basis functions for the hexahedron (the other 4 are on the back side of the hexahedra from this perspective).
Questions
While the prototype is very minimal, we hope there is enough there to spur some discussion of what works and what doesn’t.
- Are there cell types you think this approach would not handle well? What assumptions does the prototype make that are unhelpful?
- The prototype does not have a lot of traditional functionality. Rather than comment on what is missing, please comment on how you think missing features should be approached.
- Although we did not have time to pursue it with this funding, we think this approach would accommodate NURBS cells more cleanly that the existing
vtkBezierXXXcells (e.g.,vtkBezierHexahedron) since it does not preclude 4-dimensional points and knot-vector arrays tied to the “shape” field. Do you have a preference on how 4-dimensional (x,y,z,w) point-coordinates should be handled? Do you see issues with NURBS this approach cannot handle?
We hope to continue development along these lines in the future, so your feedback is really appreciated.