Hello,
Your centerline needs:
- Points in model coordinates (they take spacing, origin and direction of the ImageData into account)
This is how they are set in the example:
// Set positions of the centerline (model coordinates)
const centerlinePoints = Float32Array.from(centerlineJson.position);
const nPoints = centerlinePoints.length / 3;
centerline.getPoints().setData(centerlinePoints, 3);
- A polyline that gives the order of the points.
This is how they are set in the example:
// Set polylines of the centerline
const centerlineLines = new Uint16Array(1 + nPoints);
centerlineLines[0] = nPoints;
for (let i = 0; i < nPoints; ++i) {
centerlineLines[i + 1] = i;
}
centerline.getLines().setData(centerlineLines);
- A PointData that gives an orientation for each point. See the documentation for
getOrientationArrayName for more information.
This is how they are set in the example (using 4x4 matrices):
// Create a rotated basis data array to oriented the CPR
centerline.getPointData().setTensors(
vtkDataArray.newInstance({
name: 'Orientation',
numberOfComponents: 16,
values: Float32Array.from(centerlineJson.orientation),
})
);
centerline.modified();
Now, you also have to choose between stretched and straightened mode.
I think that for your application, the straightened mode is the way to go.
It is the default but in case you want to make sure that this mode is used:
mapper.useStraightenedMode();
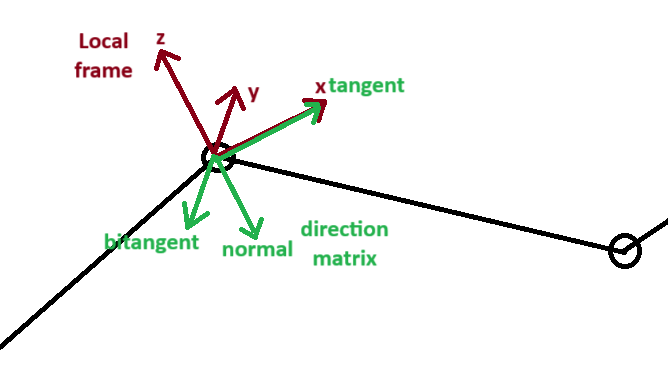
Then, you can set the direction matrix. Depending on which plane you want (transversal in your example) and the orientation you gave to your points, you will choose a 3x3 matrix. You can see this matrix as a transformation that you apply to all your points.
The most important part of this matrix is the first vector. It will determine the direction that will be used to sample voxels at each local frame. The local frame is determined by the local position and orientation given by your input centerline.
In the example below, you can see in dark red the local frame determined by position and orientation of the centerline. And in green, the direction matrix. The samples will be taken along the tangent direction. In this example the tangent direction is [1, 0, 0], the bitangent is [0, -1, 0] and the normal is [0, 0, -1]. So the direction matrix is [1, 0, 0, 0, -1, 0, 0, 0, -1].