vtkCoordinateFrameWidget

Development
1

VTK now has the vtkCoordinateFrameWidget which controls 3 orthogonal, right-handed planes.
(see VTK MR)

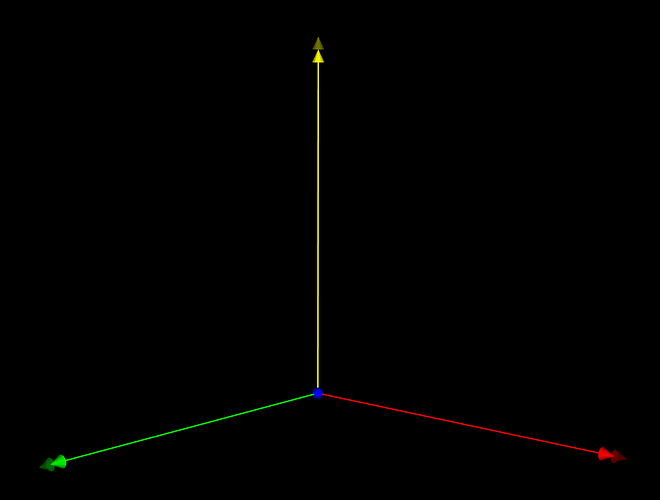
The representation of the vtkCoordinateFrameWidget can be seen below:

coordinateFrameWidget
coordinateFrameWidget1161×879 7.71 KB

In more detail, the representation of the vtkCoordinateFrameWidget has:

  1. The origin point of the coordinate frame widget is represented as a sphere.
  2. Three normal vectors of the three orthogonal planes which are represented as lines segments with a cone tip
  3. Three normal vector lockers are represented as (opaque) cone tips.

vtkCoordinateFrameWidget supports the following actions:

  1. When you interact with a widget part, its color becomes ambient to give you feedback before you interact with the
    widget
  2. When you click on normal vector locker (the first cone tip of a vector), there are two possible 2 states: unlocked,
    and locked
    1. Locking an unlocked vector locker, it converts its color to non-opaque, and locks its plane
      1. If any other vector locker is locked, it becomes unlocked, since only one plane can be locked
    2. Unlocking a locked vector locker, converts its color to opaque, and unlocks its plane
  3. When you click+drag the origin, you can translate the origin of the widget
    1. If no normal vector is locked, the origin moves on the plane of the camera
    2. If one normal vector is locked, the origin moves on the locked normal’s vector plane
  4. When you click+drag a vector tip (the second cone tip of a vector), the orientation of the widget changes
    1. If any normal vector is locked:
      1. When you click on the locked normal vector’s tip, nothing will happen
      2. When you click on one of the unlocked normal vectors’ tips, the orientation of the widget changes, but it’s
        constrained to move only on the locked normal’s vector plane
  5. When you type ‘P/p’, it resets the origin of the widget to the picking point
  6. When you type ‘N/n’, it resets one of the vector normals to the picked normal
    1. If one normal vector is locked, the corresponding normal vector is set to the picked normal
      1. The remaining normals are re-orthogonalized using the Gram-Schmidt procedure
    2. if no normal vector is locked, the normal vector closest to the picking normal (i.e. with the largest dot
      product) is set to the picked normal
      1. The remaining normals are re-orthogonalized using the Gram-Schmidt procedure
  7. When you type ‘D/d’, it resets one of the vector’s normal to the direction of a line from the origin to the picked
    point
    1. If one normal vector is locked, the corresponding normal vector is set to the direction of the line (as defined
      above)
      1. The remaining normals are re-orthogonalized using the Gram-Schmidt procedure
    2. if no normal vector is locked, the normal vector closest to the direction of the line (as defined above) (
      i.e. with the largest dot product) is set to the direction of the line
      1. The remaining normals are re-orthogonalized using the Gram-Schmidt procedure

You can test it using: test.cxx

2 Likes