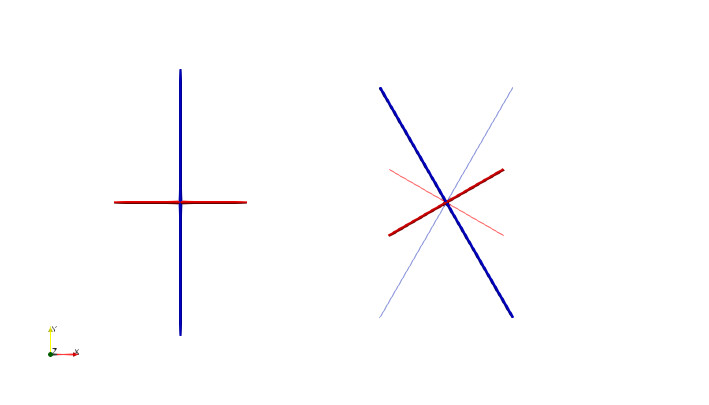Hello,
I believe there is an error in the principal vector orientations produced by vtkTensorPrincipalInvariants.
In the image below, the diagonal tensor [1, 2, 3] (left) and its version rotated counterclockwise by π/6 about the z axis (right) are shown. The externally computed correct orientation is the thick line; the orientation returned by vtkTensorPrincipalInvariants is the thin line and appears incorrect.
I suspect vtkTensorPrincipalInvariants treats eigenvectors as row-wise, whereas Diagonalize3x3 stores them column-wise. Has anyone else observed this or can confirm it?
The following script compares valid eigenpairs with vtkTensorPrincipalInvariants output.
# Compare ground-truth tensor eigenpairs with vtkTensorPrincipalInvariants output.
# - Stores tensors in VTK-native 6-component order: [Txx, Tyy, Tzz, Txy, Txz, Tyz]
# - Runs vtkTensorPrincipalInvariants, reads its Sigma arrays
# - Sorts ground-truth descending by eigenvalue and compares
# eigenvalue differences and orientation (absolute dot product).
#
import numpy as np
import vtk
# --- Parameters / ground truth ------------------------------------------------
theta = np.pi / 6.0
c, s = np.cos(theta), np.sin(theta)
R = np.array([[c, -s, 0.0],
[s, c, 0.0],
[0.0, 0.0, 1.0]])
eigvals = np.array([1.0, 2.0, 3.0]) # diagonal tensor entries (original)
T_orig = np.diag(eigvals)
T_rot = R @ T_orig @ R.T
def tensor3_to_vtk6(T):
# VTK-native 6-component order: [Txx, Tyy, Tzz, Txy, Txz, Tyz]
return (T[0,0], T[1,1], T[2,2], T[0,1], T[0,2], T[1,2])
sym_orig = tensor3_to_vtk6(T_orig)
sym_rot = tensor3_to_vtk6(T_rot)
# Ground-truth eigenvectors scaled by eigenvalues:
# original eigenvectors are standard basis columns; we store rows = each eigenvector
eigvecs_orig = (np.eye(3) * eigvals[:, None]) # shape (3,3), row i = eig i scaled
eigs_rot = (R @ np.eye(3)).T # rows are rotated eigenvectors
eigvecs_rot_scaled = eigs_rot * eigvals[:, None]
# --- Build VTK UnstructuredGrid with two points -------------------------------
points = vtk.vtkPoints()
points.InsertNextPoint(0.0, 0.0, 0.0) # point 0: original tensor
points.InsertNextPoint(2.0, 0.0, 0.0) # point 1: rotated tensor
ug = vtk.vtkUnstructuredGrid()
ug.SetPoints(points)
for pid in (0, 1):
vertex = vtk.vtkVertex()
vertex.GetPointIds().SetId(0, pid)
ug.InsertNextCell(vertex.GetCellType(), vertex.GetPointIds())
# Add symmetric tensor array (6 components) with VTK ordering
tensor6 = vtk.vtkDoubleArray()
tensor6.SetNumberOfComponents(6)
tensor6.SetName("symmetric_tensor6")
tensor6.SetNumberOfTuples(2)
tensor6.SetTuple(0, tuple(float(x) for x in sym_orig))
tensor6.SetTuple(1, tuple(float(x) for x in sym_rot))
ug.GetPointData().AddArray(tensor6)
# (optional) write input for inspection
w_in = vtk.vtkXMLUnstructuredGridWriter()
w_in.SetFileName("compare_input.vtu")
w_in.SetInputData(ug)
w_in.SetDataModeToBinary()
w_in.Write()
# --- Run vtkTensorPrincipalInvariants -----------------------------------------
tpi = vtk.vtkTensorPrincipalInvariants()
tpi.SetInputData(ug)
tpi.SetInputArrayToProcess(0, 0, 0, vtk.vtkDataObject.FIELD_ASSOCIATION_POINTS, "symmetric_tensor6")
tpi.Update()
out = tpi.GetOutput()
# --- Read TPI outputs by observed naming pattern -------------------------------
pd = out.GetPointData()
# Array names
vec_names = ["symmetric_tensor6 - Sigma 1 (Vector)",
"symmetric_tensor6 - Sigma 2 (Vector)",
"symmetric_tensor6 - Sigma 3 (Vector)"]
val_names = ["symmetric_tensor6 - Sigma 1",
"symmetric_tensor6 - Sigma 2",
"symmetric_tensor6 - Sigma 3"]
# Verify arrays exist; gather into matrices
npts = out.GetNumberOfPoints()
pv_mat = np.zeros((npts, 3), dtype=float)
pvecs_mat = np.zeros((npts, 3, 3), dtype=float) # pvecs_mat[pt, i, :] = i-th principal vector
for i in range(3):
val_arr = pd.GetArray(val_names[i])
vec_arr = pd.GetArray(vec_names[i])
for pid in range(npts):
pv_mat[pid, i] = val_arr.GetComponent(pid, 0)
pvecs_mat[pid, i, :] = [vec_arr.GetComponent(pid, c) for c in range(3)]
# --- Comparison: sort gt set descending and compare --------------------------
def unit(v):
v = np.array(v, float)
n = np.linalg.norm(v)
return v / n if n > 0 else v
for pid in range(npts):
print(f"\nPoint {pid}:")
# VTK outputs
vtk_vals = pv_mat[pid].copy()
vtk_vecs = pvecs_mat[pid].copy() # rows correspond to vtk_vals order (Sigma1..3)
# Ground truth
if pid == 0:
gt_vals = eigvals.copy()
gt_vecs = eigvecs_orig.copy()
else:
gt_vals = eigvals.copy()
gt_vecs = eigvecs_rot_scaled.copy()
# Sort Ground truth descending as tpi does
gt_idx = np.argsort(gt_vals)[::-1]
gt_vals_s = gt_vals[gt_idx]
gt_vecs_s = gt_vecs[gt_idx]
print(" vtk sorted values:", np.round(vtk_vals, 8))
print(" gt sorted values: ", np.round(gt_vals_s, 8))
print(" eigenvalue diffs (vtk - gt):", np.round(vtk_vals - gt_vals_s, 8))
print(" orientation abs-dot per component:")
for j in range(3):
vtk_dir = unit(vtk_vecs[j])
gt_dir = unit(gt_vecs_s[j])
dot = abs(np.dot(vtk_dir, gt_dir))
print(f" comp {j+1}: {dot:.8f}")