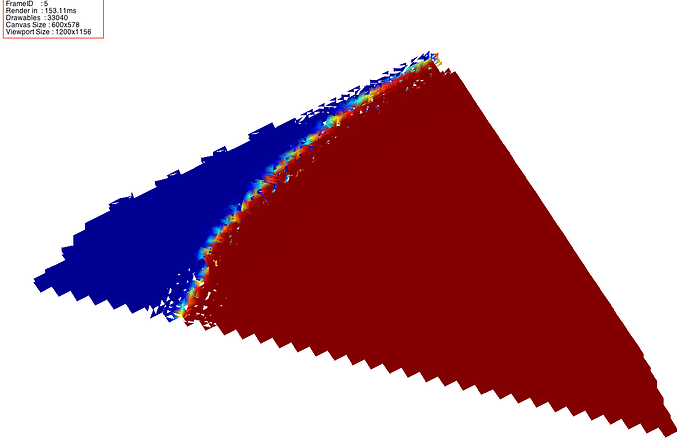
TL;DR : Would you suggest a good algorithm for reducing the number of polygons of a lego-like structure ?
I am trying to reduce the number of polygons of a vtkUnstructuredGrid containing hexahedrons which are actually lego like cubes which sizes are multiples of the smallest cubes in the geometry.
out0006.000.vtu (1.8 MB)
I expect from decimation to bundle all cubes of the same size and color and hopefully would not observe any loss of information. I observed the contrary :
- the decimation of
vtkQuadricDecimatorandvtkDecimatorProboth tend to delete small cubes that vary a lot and keep the repeating cubes. - enabling
PreserveTopologyOn()lead to no decimation at all.
Instead I obtain something like this (code later in the message)
TargetReduction = 0.8
TargetReduction = 0.9
I remember from
- the decimation chapter in the book that “CAD models typically reduce the least because these models have many sharp edges and other detailed features, and the CAD modellers usually produce minimal triangulations.”.
- this paper that “High frequencies are quantized stronger than low frequencies”
I am about to write my own algorithm that would allow lossless decimation by bundling neighbour quads of the same color and normal together. But I am sure somebody did this before. Would somebody suggest something?
Here is my (java) code to reproduce the decimation. The rendering is made with Jzy3D which provides a more stable renderer than JOGL for now… See also the dataset link above.
vtkXMLUnstructuredGridReader reader = new vtkXMLUnstructuredGridReader();
reader.SetFileName(folder + file);
reader.Update();
// -------------------------------------------
// Convert to PolyData
// https://kitware.github.io/vtk-examples/site/Cxx/PolyData/DataSetSurfaceFilter/
vtkDataSetSurfaceFilter surfaceFilter = new vtkDataSetSurfaceFilter();
surfaceFilter.SetInputConnection(reader.GetOutputPort());
surfaceFilter.Update();
// -------------------------------------------
// Make triangles
vtkTriangleFilter triangleFilter = new vtkTriangleFilter();
triangleFilter.SetInputConnection(surfaceFilter.GetOutputPort());
triangleFilter.Update();
// -------------------------------------------
// -------------------------------------------
// Decimate
vtkPolyDataAlgorithm algo;
int decimationAlgorithm = 0;
if (decimationAlgorithm == 0) {
// We want to preserve topology (not let any cracks form). This may limit
// the total reduction possible, which we have specified at 90%.
/*
* vtkDecimatePro is a filter to reduce the number of triangles in a triangle mesh, forming a
* good approximation to the original geometry. The input to vtkDecimatePro is a vtkPolyData
* object, and only triangles are treated. If you desire to decimate polygonal meshes, first
* triangulate the polygons with vtkTriangleFilter object.
*
* The implementation of vtkDecimatePro is similar to the algorithm originally described in
* "Decimation of Triangle Meshes", Proc Siggraph `92, with three major differences. First,
* this algorithm does not necessarily preserve the topology of the mesh. Second, it is
* guaranteed to give the a mesh reduction factor specified by the user (as long as certain
* constraints are not set - see Caveats). Third, it is set up generate progressive meshes,
* that is a stream of operations that can be easily transmitted and incrementally updated
* (see Hugues Hoppe's Siggraph '96 paper on progressive meshes).
*
* The algorithm proceeds as follows. Each vertex in the mesh is classified and inserted into
* a priority queue. The priority is based on the error to delete the vertex and retriangulate
* the hole. Vertices that cannot be deleted or triangulated (at this point in the algorithm)
* are skipped. Then, each vertex in the priority queue is processed (i.e., deleted followed
* by hole triangulation using edge collapse). This continues until the priority queue is
* empty. Next, all remaining vertices are processed, and the mesh is split into separate
* pieces along sharp edges or at non-manifold attachment points and reinserted into the
* priority queue. Again, the priority queue is processed until empty. If the desired
* reduction is still not achieved, the remaining vertices are split as necessary (in a
* recursive fashion) so that it is possible to eliminate every triangle as necessary.
*
* To use this object, at a minimum you need to specify the ivar TargetReduction. The
* algorithm is guaranteed to generate a reduced mesh at this level as long as the following
* four conditions are met: 1) topology modification is allowed (i.e., the ivar
* PreserveTopology is off); 2) mesh splitting is enabled (i.e., the ivar Splitting is on); 3)
* the algorithm is allowed to modify the boundary of the mesh (i.e., the ivar
* BoundaryVertexDeletion is on); and 4) the maximum allowable error (i.e., the ivar
* MaximumError) is set to VTK_DOUBLE_MAX. Other important parameters to adjust include the
* FeatureAngle and SplitAngle ivars, since these can impact the quality of the final mesh.
* Also, you can set the ivar AccumulateError to force incremental error update and
* distribution to surrounding vertices as each vertex is deleted. The accumulated error is a
* conservative global error bounds and decimation error, but requires additional memory and
* time to compute.
*/
vtkDecimatePro decimate = new vtkDecimatePro();
decimate.SetInputConnection(triangleFilter.GetOutputPort());
/*
* Specify the desired reduction in the total number of polygons (e.g., if TargetReduction is
* set to 0.9, this filter will try to reduce the data set to 10% of its original size).
*
* Because of various constraints, this level of reduction may not be realized. If you want to
* guarantee a particular reduction, you must turn off PreserveTopology, turn on SplitEdges
* and BoundaryVertexDeletion, and set the MaximumError to VTK_DOUBLE_MAX (these ivars are
* initialized this way when the object is instantiated).
*/
decimate.SetTargetReduction(0.5);
/*
* Turn on/off whether to preserve the topology of the original mesh.
*
* If on, mesh splitting and hole elimination will not occur. This may limit the maximum
* reduction that may be achieved.
*/
decimate.PreserveTopologyOff();
/*
* Turn on/off the deletion of vertices on the boundary of a mesh.
*
* This may limit the maximum reduction that may be achieved.
*/
decimate.BoundaryVertexDeletionOn();
/*
* Turn on/off the splitting of the mesh at corners, along edges, at non-manifold points, or
* anywhere else a split is required.
*
* Turning splitting off will better preserve the original topology of the mesh, but you may
* not obtain the requested reduction.
*/
decimate.SplittingOn();
/*
* Specify the mesh split angle.
*
* This angle is used to control the splitting of the mesh. A split line exists when the
* surface normals between two edge connected triangles are >= SplitAngle.
*/
decimate.SetSplitAngle(30);
/*
* In some cases you may wish to split the mesh prior to algorithm execution.
*
* This separates the mesh into semi-planar patches, which are disconnected from each other.
* This can give superior results in some cases. If the ivar PreSplitMesh ivar is enabled, the
* mesh is split with the specified SplitAngle. Otherwise mesh splitting is deferred as long
* as possible.
*/
decimate.PreSplitMeshOn();
/*
* Set the largest decimation error that is allowed during the decimation process.
*
* This may limit the maximum reduction that may be achieved. The maximum error is specified
* as a fraction of the maximum length of the input data bounding box.
*
* Max value is 1.0e+299
*
* https://vtk.org/doc/nightly/html/vtkType_8h.html#aa933eb1ff8ef089de59cce7b41e21261
*/
decimate.SetMaximumError(1.0e+299);
/*
* Specify the mesh feature angle.
*
* This angle is used to define what an edge is (i.e., if the surface normal between two
* adjacent triangles is >= FeatureAngle, an edge exists).
*/
decimate.SetFeatureAngle(30);
/*
* The computed error can either be computed directly from the mesh or the error may be
* accumulated as the mesh is modified.
*
* If the error is accumulated, then it represents a global error bounds, and the ivar
* MaximumError becomes a global bounds on mesh error. Accumulating the error requires extra
* memory proportional to the number of vertices in the mesh. If AccumulateError is off, then
* the error is not accumulated.
*/
decimate.AccumulateErrorOn();
/*
* If the number of triangles connected to a vertex exceeds "Degree", then the vertex will be
* split.
*
* (NOTE: the complexity of the triangulation algorithm is proportional to Degree^2. Setting
* degree small can improve the performance of the algorithm.)
*/
decimate.SetDegree(20);
/*
* Specify the inflection point ratio.
*
* An inflection point occurs when the ratio of reduction error between two iterations is
* greater than or equal to the InflectionPointRatio.
*/
decimate.SetInflectionPointRatio(10);
TicToc.tick();
decimate.Update();
TicToc.tockShow("Decimation took");
algo = decimate;
} else if (decimationAlgorithm == 1) {
/*
* vtkQuadricDecimation is a filter to reduce the number of triangles in a triangle mesh,
* forming a good approximation to the original geometry. The input to vtkQuadricDecimation is
* a vtkPolyData object, and only triangles are treated. If you desire to decimate polygonal
* meshes, first triangulate the polygons with vtkTriangleFilter.
*
* The algorithm is based on repeated edge collapses until the requested mesh reduction is
* achieved. Edges are placed in a priority queue based on the "cost" to delete the edge. The
* cost is an approximate measure of error (distance to the original surface)–described by the
* so-called quadric error measure. The quadric error measure is associated with each vertex
* of the mesh and represents a matrix of planes incident on that vertex. The distance of the
* planes to the vertex is the error in the position of the vertex (originally the vertex
* error iz zero). As edges are deleted, the quadric error measure associated with the two end
* points of the edge are summed (this combines the plane equations) and an optimal collapse
* point can be computed. Edges connected to the collapse point are then reinserted into the
* queue after computing the new cost to delete them. The process continues until the desired
* reduction level is reached or topological constraints prevent further reduction. Note that
* this basic algorithm can be extended to higher dimensions by taking into account variation
* in attributes (i.e., scalars, vectors, and so on).
*
* This paper is based on the work of Garland and Heckbert who first presented the quadric
* error measure at Siggraph '97 "Surface Simplification Using Quadric Error Metrics". For
* details of the algorithm Michael Garland's Ph.D. thesis is also recommended. Hughues
* Hoppe's Vis '99 paper,
* "New Quadric Metric for Simplifying Meshes with Appearance Attributes" is also a good take
* on the subject especially as it pertains to the error metric applied to attributes.
*/
vtkQuadricDecimation decimate = new vtkQuadricDecimation();
decimate.SetInputConnection(triangleFilter.GetOutputPort());
/*
* Decide whether to activate volume preservation which greatly reduces errors in triangle
* normal direction.
*
* If off, volume preservation is disabled and if AttributeErrorMetric is active, these errors
* can be large. By default VolumePreservation is off the attribute errors are off.
*/
decimate.VolumePreservationOn();
/*
* Decide whether to include data attributes in the error metric.
*
* If off, then only geometric error is used to control the decimation. By default the
* attribute errors are off.
*/
decimate.AttributeErrorMetricOn();
//
// NB : setting to OFF does not allow retrieving attributes (point color) in the output dataset
//
/*
* If attribute errors are to be included in the metric (i.e., AttributeErrorMetric is on),
* then the following flags control which attributes are to be included in the error
* calculation.
*
* By default all of these are on.
*/
decimate.ScalarsAttributeOn();
/*
* If attribute errors are to be included in the metric (i.e., AttributeErrorMetric is on),
* then the following flags control which attributes are to be included in the error
* calculation.
*
* By default all of these are on.
*/
decimate.VectorsAttributeOn();
/*
* If attribute errors are to be included in the metric (i.e., AttributeErrorMetric is on),
* then the following flags control which attributes are to be included in the error
* calculation.
*
* By default all of these are on.
*/
decimate.NormalsAttributeOn();
/*
* If attribute errors are to be included in the metric (i.e., AttributeErrorMetric is on),
* then the following flags control which attributes are to be included in the error
* calculation.
*
* By default all of these are on.
*/
decimate.TCoordsAttributeOn();
/*
* If attribute errors are to be included in the metric (i.e., AttributeErrorMetric is on),
* then the following flags control which attributes are to be included in the error
* calculation.
*
* By default all of these are on.
*/
decimate.TensorsAttributeOn();
/*
* Set/Get the desired reduction (expressed as a fraction of the original number of
* triangles).
*
* The actual reduction may be less depending on triangulation and topological constraints.
*/
decimate.SetTargetReduction(.75);
decimate.Update();
algo = decimate;
} else {
throw new IllegalArgumentException("not an algo " + decimationAlgorithm);
}
System.out.println("INPUT");
System.out.println(reader.GetOutput().GetNumberOfPoints() + " points in output");
System.out.println(reader.GetOutput().GetNumberOfCells() + " cells in output");
System.out.println("POLYGONS");
System.out.println(surfaceFilter.GetOutput().GetNumberOfPoints() + " points in output");
System.out.println(surfaceFilter.GetOutput().GetNumberOfCells() + " cells in output");
System.out.println("TRIANGLES");
System.out.println(triangleFilter.GetOutput().GetNumberOfPoints() + " points in output");
System.out.println(triangleFilter.GetOutput().GetNumberOfCells() + " cells in output");
System.out.println("DECIMATED");
System.out.println(algo.GetOutput().GetNumberOfPoints() + " points in output");
System.out.println(algo.GetOutput().GetNumberOfCells() + " cells in output");