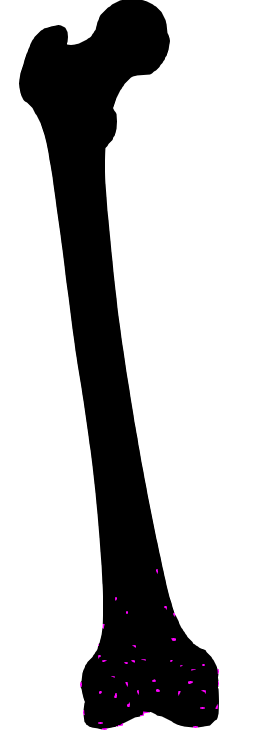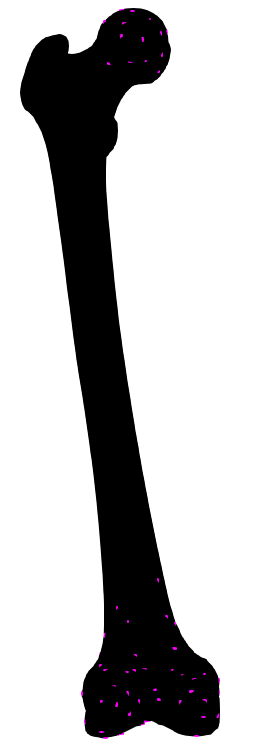Geometry in ICP registration

[maedeh_kafiyan_safar (maedeh kafiyan safary)]

I am currently using the Iterative Closest Point (ICP) algorithm provided by the VTK library for my 3D bone model. I have a set of 60 points from one part of the object, and I am trying to register them. Below is an image showing the current configuration, where the bottom part of the object is at the origin (0, 0, 0):

Next, I add more points from the other side of the object, as shown in the following image:

I expected that adding more information would decrease the registration error (note: when I say “registration error,” I am referring to the error based on the transformation matrix I compute, not the ICP algorithm itself). For example, if my target transformation is a rotation of (0, 0, 50) in each axis and (0, 0, 0) for the translation, I calculate the error based on this target transformation.

However, the results show that the error actually increases when I add more points from the top of the object. And it dosen’t matter how many points I add, It increases. I don’t understand why this is happening, as ICP appears to be working well. Could this be due to the geometry of the object or the distance between points? I am trying to figure out why adding more points leads to a higher error, despite expecting the opposite outcome.

[Paulo_Carvalho]

Hello,

It would be more helpful if you present the error in quantitative terms.

best,

PC

[maedeh_kafiyan_safar (maedeh kafiyan safary)]

well I started by adding 1 points first from top of my object, then I added 2, 4, and 38.
so the target is ( 0 50 0) for rotation in each axis and (0 0 0) translation in each axis.

The value of transformation in degree. This for when we only have noisy points from downside of the object: (1.4430487187014935, 50.3253627710147, -4.117078268025638) for rotation and (-0.009903441059789436, 0.015515333391755056, -0.004191277274364499) for translation.

This for when we only have noisy points from downside of the object and 1 points from the top (femural head) of the object: (-3.03263565001833, 49.13242519927493, -12.936139501637788) for rotation and (-0.02159234191667279, 0.02785795498978267, 0.0017078677596180163) for translation.

This for when we only have noisy points from downside of the object and 2 points from the top (femural head) of the object: (-8.554540787106733, 48.72263804041764, -11.674963100327274) for rotartion and ( -0.01459678470011031, 0.018693283901866937, 0.005130429505488484) for translation.

This for when we only have noisy points from downside of the object and 4 points from the top (femural head) of the object: (-7.145962495251272, 50.153515587021964, -9.551605106729538) for rotation and (-0.011042883971687107, 0.015393698414345605, 0.007157813601390137) for translation.

This for when we only have noisy points from downside of the object and 38 points from the top (femural head) of the object: (-3.2029093617427264, 49.97102719034115, -4.547556606783885) for rotation and (-0.00560672415229054, 0.009849018720321616, -0.0006722720538804597) for translation.

So as you can see there the error incresing alot when we add points.

[Paulo_Carvalho]

Hi,

From my experience, those results are very good to me. Unless (highy unlikely) the sample points match exactly points of the model, one must expect fluctuations. ICP finds a rigid transform, so, one must expect a best fit. Notice best ≠ exact, you know. It’s like fitting a linear model y = ax + b to a set of sample points that almost never happen to form a straight line. I mean, it’s very unlikely that a sample set matches a model, hence the results observed. In addition, the increase in error with more samples is also expected but it should have an asymptotic increase (plot number of samples versus error).

best,

PC

[maedeh_kafiyan_safar (maedeh kafiyan safary)]

@Paulo_Carvalho

From my experience, those results are very good to me. Unless (highy unlikely) the sample points match exactly points of the model, one must expect fluctuations. ICP finds a rigid transform, so, one must expect a best fit. Notice best ≠ exact, you know. It’s like fitting a linear model y = ax + b to a set of sample points that almost never happen to form a straight line. I mean, it’s very unlikely that a sample set matches a model, hence the results observed. In addition, the increase in error with more samples is also expected but it should have an asymptotic increase (plot number of samples versus error).

I understand the general principle you’re describing with ICP. But, I think my situation differs in a key respect that the points I’m using from the top of the object aren’t noisy samples.
The points I’ve selected from the top of the object are taken directly from the exact vertices of the cells on the surface. Since these points are precisely on the model surface without any noise, I would expect that adding more of these “perfect” points should either:

1. Decrease the registration error (by providing more accurate constraints)
2. At minimum, not increase the error

But what I’m seeing is that even when I add up to 100 of these noiseless points from the top surface, the error continues to increase. This seems counterintuitive to me. I don’t understand why you mentioned the increase in error with more samples is also expected .
If ICP is finding the best rigid transformation to align perfect points from the same model, why would more perfect information lead to worse results?
Could there be something else happening in the registration process that explains this behavior? like the distribution of points?

[Paulo_Carvalho]

Hello,

You must also consider that your samples are not equally distributed over the entire domain. I mean, your samples are clustered (e.g. concentrated in the femur’s head and condyles area) and that likely adds up to the overall error. Perhaps you could try to take random samples from the entire bone model if your objective is to evaluate or benchmark the performance of the implementation.

take care,

PC

[Paulo_Carvalho]

Also consider that ICP, as the name implies, is an iterative optimization algorithm. That means it runs in a loop until a convergence criterion is met. The convergence is controlled by setting some parameters of the vtkIterativeClosestPointTransform object. Hence, these parameters often severely impact the result. As general rule, iterative optimization has a tradeoff between speed and accuracy. Maybe you could study the class’ API: VTK: vtkIterativeClosestPointTransform Class Reference and become acquainted with the parameters in case you haven’t done so already.