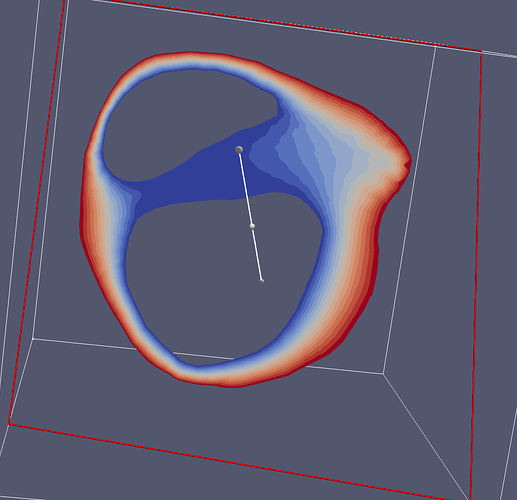
I have a model of the human heart represented by a surface mesh. I solve the Laplace differential equation to calculate the wall thickness on this domain. The solution is saved in vtu format and is a volumetric mesh. Below is an example of slice of the heart with the equation solved (with 16-color discretisation).
Here’s also an explanation of why you should use the Laplace equation to calculate heart wall thickness.
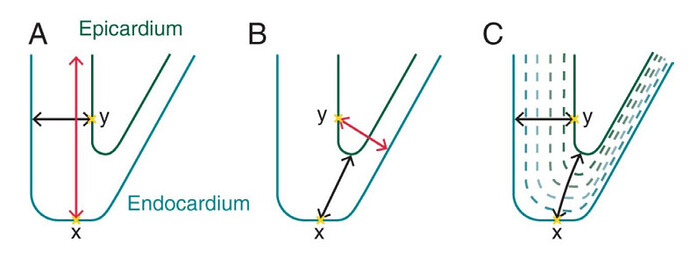
A - calculation through the normal to the surface
B - calculation through KDTree
C - calculation through Laplace’s equation
My question is how to get the distance between two points given the gradient (Laplace’s equation solution). My idea is to take a 0.5 level isoline (the middle of the heart wall) and use something like gradient descent to find intersections with each of the walls. Then the sum of the lengths of the vectors will be the length of the heart wall. How can I use vtk to solve this? Is there a simpler solution?