Introduction
The Dual Contouring / Surface Nets algorithm (specifically the VTK implementation through Pyvista’s contour_labels method) occasionally generates meshes with non-manifold edges for specific scenarios. We have been trying to solve this problem without success and are looking for information about if this problem has already been solved or if anyone has advice on how this could be solved.
Problem
The Dual Contouring / Surface Nets algorithms can generate non-manifold edges for voxels on a surface that are diagonal. As far as my understanding, an edge on a surface mesh should ideally only connect to 2 faces. However, the edges in this problem connect to 4 faces. This makes it easy to identify problematic edges programmatically. It is challenging to describe this problem in words, so we compiled a set of GIFs demonstrating the problem below.
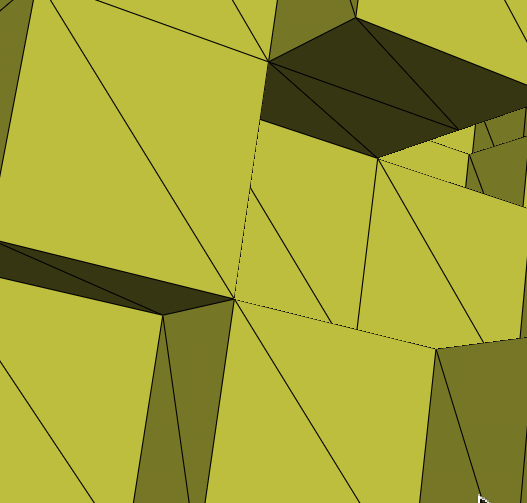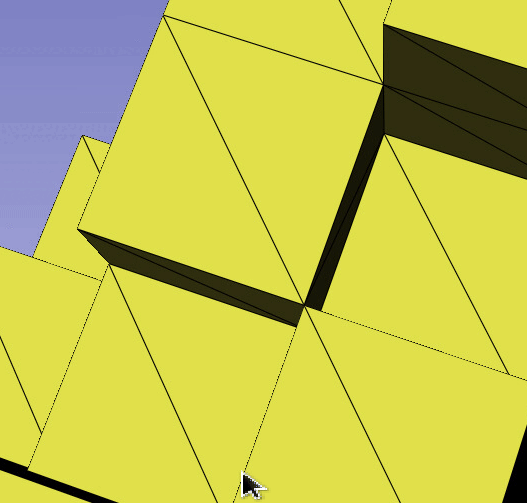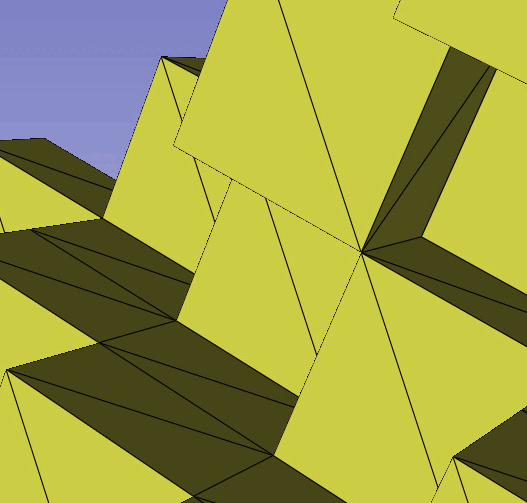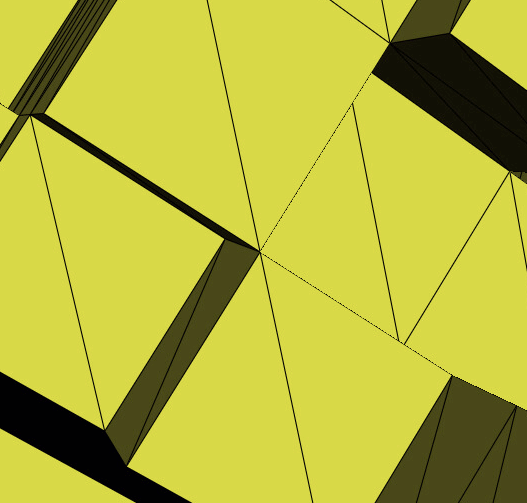

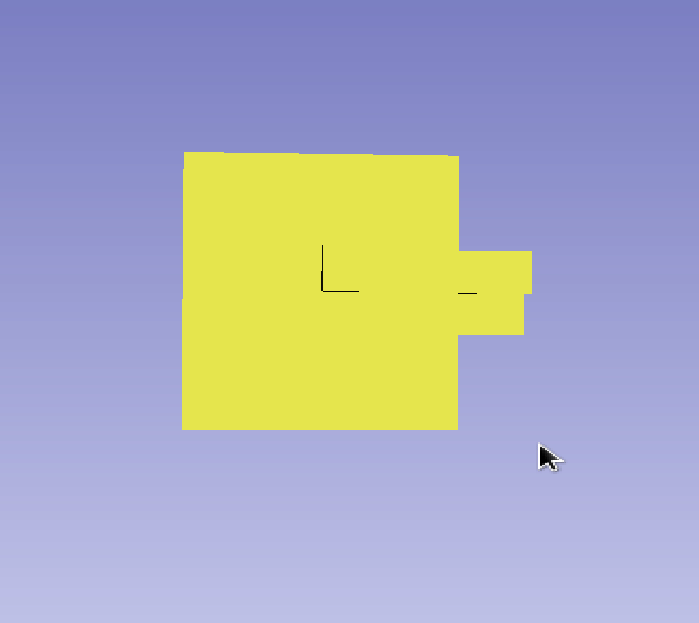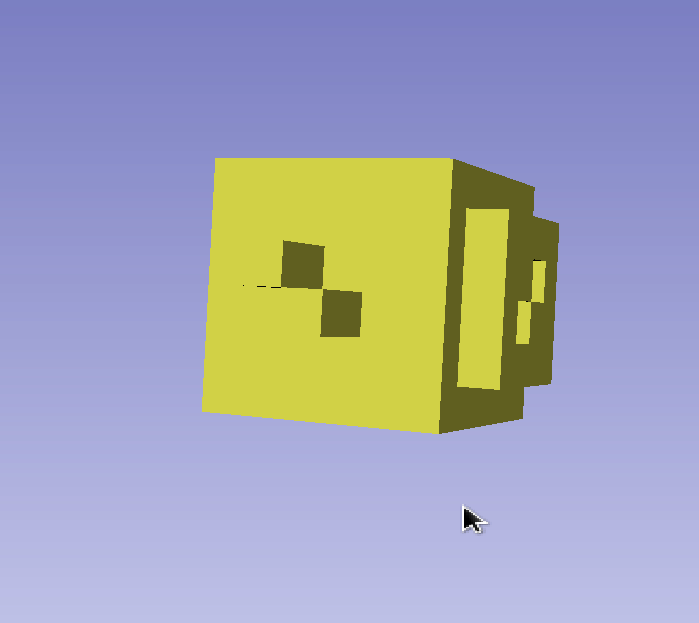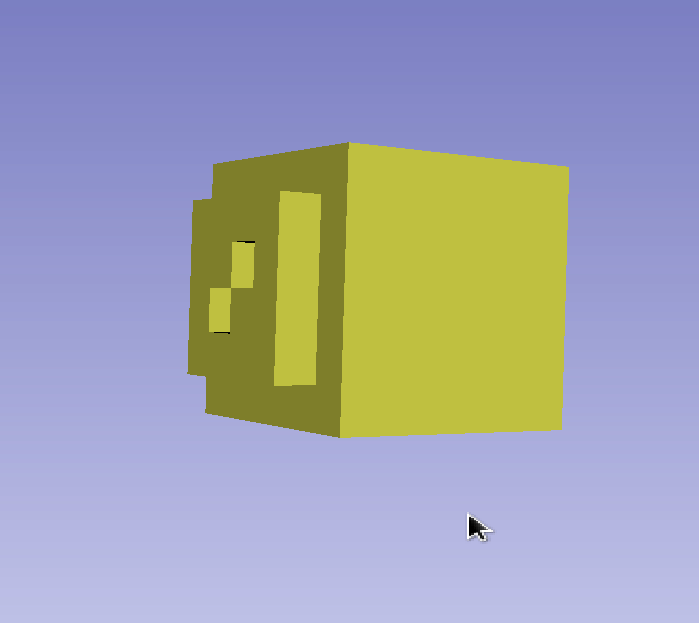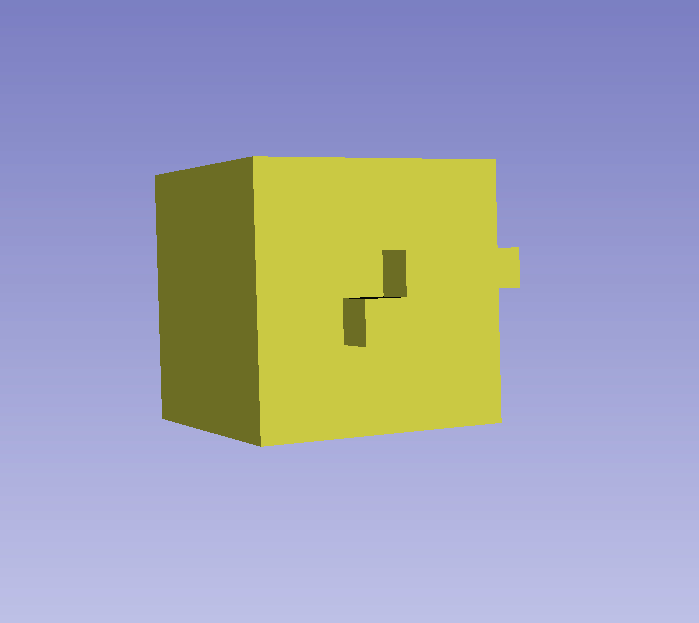
This isn’t a problem with many operations, such as computing the volume. However, some other operations do not work well with these non-manifold edges. For example, we used Laplacian smoothing (from Trimesh.smoothing) on some generated meshes that contained these problems and it creates sharp spikes extruding from the surface, originating from these non-manifold edges. Additionally, Trimesh reports these meshes as not watertight. Below is a GIF demonstrating a sharp spike generated from the Laplacian smoothing operation applied to a mesh with a non-manifold edge.

Code
Below is a snippet of code we generated that demonstrates every case of non-manifold edges that we could think of for testing potential solutions on.
import numpy as np
import trimesh
import pyvista as pv
def to_mesh(data: np.ndarray) -> trimesh.Trimesh:
# Convert a Numpy array to a mesh using Surface Nets from Pyvista/VTK
data: pv.ImageData = pv.wrap(data)
mesh = data.contour_labels(output_mesh_type="triangles", smoothing=False)
faces = mesh.faces.reshape((mesh.n_cells, 4))[:, 1:]
mesh = trimesh.Trimesh(mesh.points, faces)
mesh.fix_normals()
if mesh.volume < 0:
mesh.invert()
return mesh
# Create initial data
data = np.zeros((10, 10, 10))
data[2:-2, 2:-2, 2:-2] = 1
# Case 1 - simple extrusion
data[1, 4, 4] = 1
data[1, 5, 5] = 1
# Case 2 - simple indentation
data[-2, 3, 3] = 1
data[-2, 3, 4] = 1
data[-2, 4, 3] = 1
data[-2, 4, 4] = 1
data[-2, 5, 5] = 1
data[-2, 5, 6] = 1
data[-2, 6, 5] = 1
data[-2, 6, 6] = 1
data[-2, 4, 6] = 1
data[-2, 3, 6] = 1
data[-2, 3, 5] = 1
data[-2, 5, 3] = 1
data[-2, 6, 3] = 1
data[-2, 6, 4] = 1
# Case 3 - double extrusion
data[4, 4, 1] = 1
data[4, 4, 0] = 1
data[5, 5, 1] = 1
data[5, 5, 0] = 1
# Convert the data to a mesh and show it
mesh = to_mesh(data)
print(f"Volume: {mesh.volume}")
print(f"Watertight: {mesh.is_watertight}")
# mesh.export("test.stl")
mesh.show()
Our Research
We had some internal brainstorming sessions to try to come up with potential solutions to fix this problem and came up with the idea described below, but struggled with developing it into a real implementation.
- Identify non-manifold edges (edges shared by 4 faces)
- Determine the upper vertex (outward facing)
- This is challenging and our best idea is to try one, check if the result creates a hole, and if it does, select the other
- Split the vertex into 2 slightly separated vertices (1e-8 or something)
- This is also tricky, since you need to separate the vertices in the proper direction (away from each other)
- One idea for the determining the direction is to:
- Group the 4 faces connected to the non-manifold edge based on whether their normals are perpendicular and facing away from each other
- Taking the average of the remaining vertices positions from each set of faces that are not on the non-manifold edge
- Moving the vertices in this direction
- Update each face that was connected to the original vertex to the closest new vertex
- Take the average vertex position
- Find the closer new vertex to connect it to
Any ideas would be appreciated. We feel that the Surface Nets algorithm is popular enough and has been around long enough that this problem may have already been solved, but are struggling to find information on it.
We also posted this question to StackOverflow here.