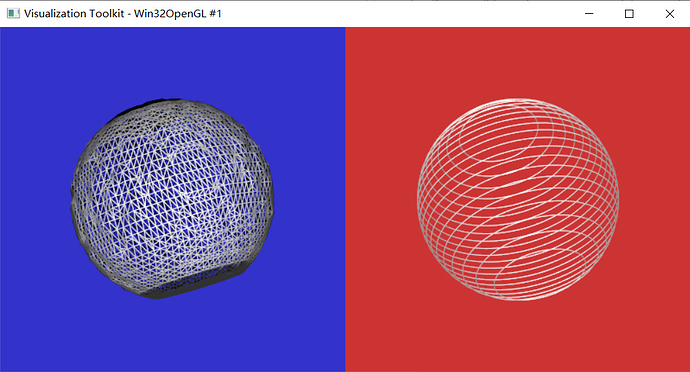
I have a set of contour, and I want to convert the contours to surface. However, the contours are not paralleled. The created surface should be a bend tube. Is there any class in VTK can implement this function?
@zhang-qiang-github did you see the Marching Cubes Example: https://lorensen.github.io/VTKExamples/site/Cxx/Modelling/MarchingCubes/ This allows you to select the contours you use.
The marching cube allows to extract the iso-surface from a volume image. However, I want to generate the surface from a set of contours. There is an example to generate surface from a set of contours.
However, this example required the set of contour should be the paralleled, like:
for (int i = 0; i < resolution; ++i)
{
double theta = vtkMath::RadiansFromDegrees(360. * i / double(resolution));
double x = radius * cos(theta);
double y = radius * sin(theta);
points->SetPoint(i, x, y, z);
cells->InsertCellPoint(i);
}
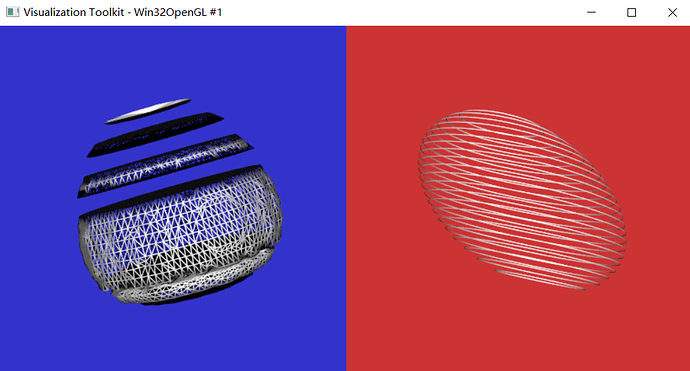
If I make the contours to not be paralleled by:
points->SetPoint(i, x, y, z+x/2);
Then, the surface is wrong:
How can I generate the surface by a set of contours which are not paralleled?
And the code to generate the wrong surface is:
#include <vtkActor.h>
#include <vtkAppendPolyData.h>
#include <vtkCellArray.h>
#include <vtkMath.h>
#include <vtkPolyData.h>
#include <vtkPolyDataMapper.h>
#include <vtkProperty.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkRenderer.h>
#include <vtkSmartPointer.h>
#include <vtkTransform.h>
#include <vtkTransformPolyDataFilter.h>
#include <vtkVoxelContoursToSurfaceFilter.h>
#include <vtkMarchingCubes.h>
#include <vtkInteractorStyleTrackballCamera.h>
void CreateCircle(const double& z, const double& radius, const int& resolution,
vtkPolyData* polyData);
int main(int, char*[])
{
// Create the data: a series of discs representing the intersections of x-y
// planes through a unit sphere centered at 0, 0, 0
//
int numDivisions = 20;
int resolution = 100;
double lastz = 0.0;
double z = 0.0;
// double radius = 0.0;
double sphereRadius = 1.0;
double zmin = -0.9 * sphereRadius;
double zmax = 0.9 * sphereRadius;
// Append all the discs into one polydata
//
auto appendFilter = vtkSmartPointer<vtkAppendPolyData>::New();
for (int i = 0; i <= numDivisions; ++i)
{
lastz = z;
double u = i / double(numDivisions);
z = (1. - u) * zmin + u * zmax;
auto radius = sqrt(sphereRadius * sphereRadius - z * z);
auto circle = vtkSmartPointer<vtkPolyData>::New();
CreateCircle(z, radius, resolution, circle);
appendFilter->AddInputData(circle);
}
double deltaz = z - lastz;
if (!appendFilter->GetNumberOfInputConnections(0))
{
cerr << "error, no contours!" << endl;
return EXIT_FAILURE;
}
appendFilter->Update();
// Convert to ijk coordinates for the contour to surface filter
//
double bounds[6];
vtkPolyData* contours = appendFilter->GetOutput();
contours->GetBounds(bounds);
double origin[3] = {bounds[0], bounds[2], bounds[4]};
double spacing[3] = {(bounds[1] - bounds[0]) / 40,
(bounds[3] - bounds[2]) / 40, deltaz};
auto poly = vtkSmartPointer<vtkPolyData>::New();
auto points = vtkSmartPointer<vtkPoints>::New();
vtkPoints* contourPoints = contours->GetPoints();
int numPoints = contourPoints->GetNumberOfPoints();
points->SetNumberOfPoints(numPoints);
for (int i = 0; i < numPoints; ++i)
{
double pt[3];
contourPoints->GetPoint(i, pt);
pt[0] = static_cast<int>((pt[0] - origin[0]) / spacing[0] + 0.5);
pt[1] = static_cast<int>((pt[1] - origin[1]) / spacing[1] + 0.5);
pt[2] = static_cast<int>((pt[2] - origin[2]) / spacing[2] + 0.5);
points->SetPoint(i, pt);
}
poly->SetPolys(contours->GetPolys());
poly->SetPoints(points);
// Create the contour to surface filter
//
auto contoursToSurface =
vtkSmartPointer<vtkVoxelContoursToSurfaceFilter>::New();
contoursToSurface->SetInputData(poly);
contoursToSurface->SetSpacing(spacing[0], spacing[1], spacing[2]);
contoursToSurface->Update();
// Rescale the output back into world coordinates and center it
//
double scaleCenter[3];
contoursToSurface->GetOutput()->GetCenter(scaleCenter);
double scaleBounds[6];
contoursToSurface->GetOutput()->GetBounds(scaleBounds);
double center[3];
contours->GetCenter(center);
auto transformFilter = vtkSmartPointer<vtkTransformPolyDataFilter>::New();
transformFilter->SetInputConnection(contoursToSurface->GetOutputPort());
auto transform = vtkSmartPointer<vtkTransform>::New();
transformFilter->SetTransform(transform);
transform->Translate(-scaleCenter[0], -scaleCenter[1], -scaleCenter[2]);
transform->Scale((bounds[1] - bounds[0]) / (scaleBounds[1] - scaleBounds[0]),
(bounds[3] - bounds[2]) / (scaleBounds[3] - scaleBounds[2]),
(bounds[5] - bounds[4]) / (scaleBounds[5] - scaleBounds[4]));
transform->Translate(center[0], center[1], center[2]);
// Visualize the contours
//
auto contoursMapper = vtkSmartPointer<vtkPolyDataMapper>::New();
contoursMapper->SetInputData(contours);
contoursMapper->ScalarVisibilityOff();
auto contoursActor = vtkSmartPointer<vtkActor>::New();
contoursActor->SetMapper(contoursMapper);
contoursActor->GetProperty()->SetRepresentationToWireframe();
contoursActor->GetProperty()->ShadingOff();
// Visualize the surface
//
auto surfaceMapper = vtkSmartPointer<vtkPolyDataMapper>::New();
surfaceMapper->SetInputConnection(contoursToSurface->GetOutputPort());
//surfaceMapper->SetInputConnection(transformFilter->GetOutputPort());
surfaceMapper->ScalarVisibilityOff();
auto surfaceActor = vtkSmartPointer<vtkActor>::New();
surfaceActor->SetMapper(surfaceMapper);
surfaceActor->GetProperty()->SetRepresentationToWireframe();
surfaceActor->GetProperty()->ShadingOff();
// Create two renderers side by side to show the contours and the surface
// separately
//
// Press 't' for trackball interaction
// Press 'r' to reset the camera
// Press 'w' for wireframe representation
// Press 's' for surface representation
//
auto renderer1 = vtkSmartPointer<vtkRenderer>::New();
renderer1->SetViewport(0., 0., 0.5, 1.);
renderer1->SetBackground(0.2, 0.2, 0.8);
auto renderer2 = vtkSmartPointer<vtkRenderer>::New();
renderer2->SetViewport(0.5, 0., 1., 1.);
renderer2->SetBackground(0.8, 0.2, 0.2);
auto renderWindow = vtkSmartPointer<vtkRenderWindow>::New();
renderWindow->SetSize(800, 400);
renderWindow->AddRenderer(renderer1);
renderWindow->AddRenderer(renderer2);
auto interactor = vtkSmartPointer<vtkRenderWindowInteractor>::New();
interactor->SetRenderWindow(renderWindow);
auto style = vtkSmartPointer<vtkInteractorStyleTrackballCamera>::New();
interactor->SetInteractorStyle(style);
renderer1->AddViewProp(surfaceActor);
renderer2->AddViewProp(contoursActor);
renderWindow->Render();
interactor->Start();
return EXIT_SUCCESS;
}
void CreateCircle(const double& z, const double& radius, const int& resolution,
vtkPolyData* polyData)
{
auto points = vtkSmartPointer<vtkPoints>::New();
auto cells = vtkSmartPointer<vtkCellArray>::New();
points->SetNumberOfPoints(resolution);
cells->Allocate(1, resolution);
cells->InsertNextCell(resolution);
for (int i = 0; i < resolution; ++i)
{
double theta = vtkMath::RadiansFromDegrees(360. * i / double(resolution));
double x = radius * cos(theta);
double y = radius * sin(theta);
points->SetPoint(i, x, y, z+x/2);
cells->InsertCellPoint(i);
}
polyData->Initialize();
polyData->SetPolys(cells);
polyData->SetPoints(points);
}
You may have branching, some branches may terminate, some others may join others again, there may be internal holes, etc. which make it impossible to create a general algorithm that can optimally reconstruct any set of contours into a surface - even if all the contours are on parallel planes.
If you have a very special case, such as a single tube (no branching), number of points in each contour are the same, corresponding points in the contours have the same ID then you can easily create a surface between the contours by defining a triangle strip. If you don’t have the same number of points then you can oversample the contours that have less points. If points IDs don’t match initially then you can develop a corresponding point finding method (e.g., based on closest distance).
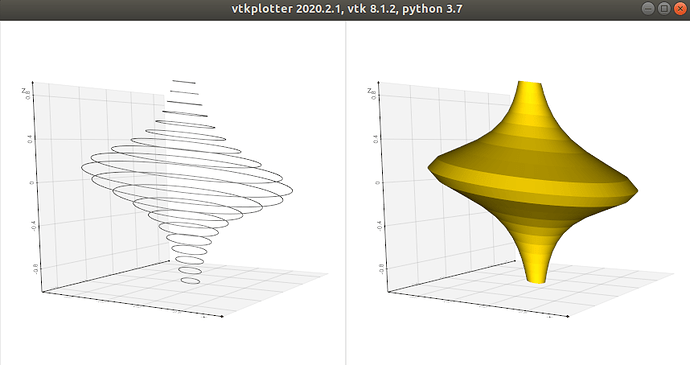
What about using vtkRuledSurfaceFilter, here is a possible recipe, where nr of points do not need match:
import numpy as np
from vtkplotter import *
cs = []
for i in range(-10,10):
r = 10/(i*i+10)
c = Circle(r=r).wireframe().rotateY(10).z(i/10)
cs.append(c)
rbs =[]
for i in range(len(cs)-1):
rb = Ribbon(cs[i], cs[i+1], res=(200,5))
rbs.append(rb)
mesh = merge(rbs)
show([cs, mesh], N=2, axes=1)
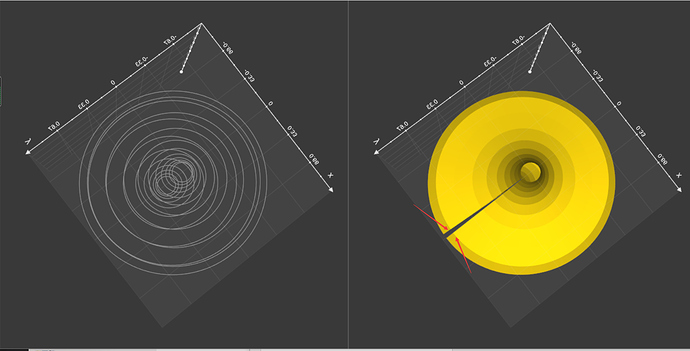
Thank you very much, and I have tested the code. However, I find something very strange:
Why the surface is not closed?
i think it is just because in the example the last point is not set as the first point, but that would not be an issue in your case as you pass the coordinates of the contours yourself.
Thank you very much. Could you please provde an example about how to define a triangle strip? And after finding the closest point, how can I match the ID and create the surface? Could you please give me an example? It would really help me a lot.
You can have a look at vtkRuledSurfaceFilter implementation in VTK or 3D Slicer’s planar contour to closed surface converter.