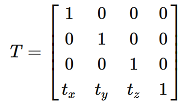Hello,
I am using vtkProcrustesAlignmentFilter to align two polydata to their mutual mean. After applying this filter, is it possible to get the information of their transformation values -rotation and translation in particular?
Thank you in advance for any feedback you could provide 
If I remember well, vtkProcrustesAlignmentFilter is for groupwise analysis. You can use vtkLandmarkTransform or vtkIterativeClosestPointTransform to align two meshes.
Hello, Gabriella,
Let:
A an n x 3 matrix composed by the n known x,y,z coordinates of the original data set.B an n x 3 composed by the n known x,y,z coordinates of the data set in its final position.First compute the center of gravities (c.g.) for both data sets by simply computing the mean of their x,y,z coordinates. Each c.g. is a single x,y,z tuple. The -x,-y,-z of them give you both translation matrices TA, and TB, which have this shape:
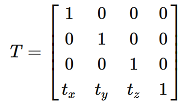
Now, bring both data sets to the origin (0,0,0) by subtracting the x,y,z’s of A and B by their respective c.g.‘s. The resulting data sets are A’ and B’. Now, let’s find the rotation matrix:
In 3D space your problem can be defined as this equation in matrix form: A'X = B', where X is the unknown 3 x 3 transform matrix.
To find the unknown 3x3 transform, you need of course at least three points in your data set. Then, isolate X:
A’-1A’X = A’-1B’
X = A’-1B’
Transpose A’-1 so it becomes a 3 x n matrix to be multipliable by the B' matrix.
Well, for real-world problems, A' won’t be square, so you can compute its pseudoinverse by using SVD (single value decomposition) to obtain three matrices:
svd(A’) = UΣV*
The asterisk symbol denotes a conjugate transpose of the matrix. If your values are not complex, then it denotes only the transpose matrix.
The pseudoinverse of A', termed A’†, can be found by doing:
A’† = VΣ†U*, where:
Then do X = A’†B’. Note that X is a matrix that may contain combined transforms. To find the rotation matrix, do an svd on X:
svd(X) = UΣV*
The rotation matrix R is simply R = VU*.
Computaionally, the Eigen library can be used to calculate these svd’s (Eigen: SVD module). Eigen is a header-only library so it’s easy to add to your project. The other matrix operations can be easily done with Eigen itself, VTK, Boost or one of the C++'s standard libraries.
I hope this helps,
Paulo
Assuming the transform is rigid, that is: without shear, scaling and/or deformation, your final transform matrix is:
Y = TBRTA.
R is a 3x3 matrix. To become multiplication-compatible with the translation ones, just add a [0,0,0,1] column to the right of R and a [0,0,0,1] row to the bottom of R, so it has this shape:
Hi Paulo,
Thank you for spending your time explaining me exactly was I was looking for. I am working on implementing this solution in python. I will post it here once I am done.
You’re quite welcome! This procedure may have mistakes in details such as signals or matrix dimensions. If you find them, please, be so kind as to report them here so we can correct them. Any peer reviews on this will be much appreciated!
@Paulo_Carvalho is the algorithm you described the Horn method? As I wrote above, that is available in vtkLandmarkTransform - ready to be used in both C++ and Python, for computing rigid, scaling, and affine transform and its inverse, directly from vtkPoints objects.
It is useful to understand the underlying basic algorithms and maybe even reimplementing them as a learning exercise, but for production use, most users will just want to use the existing robust, well-tested, optimized implementations in VTK registration classes.
I think the OP wanted the separate components of the transform. As far as I know, vtkLandmarkTransform yields the final transform matrix. So, one still has to use SVD or some other factorization method to get the individual matrices.