Non-shrinking (Taubin-) smoothing for lines?

Support
1

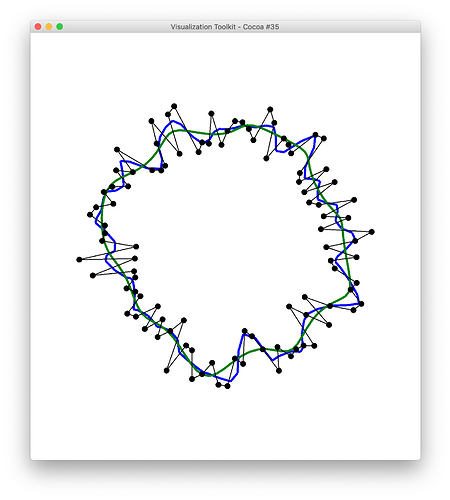
I’m using vtkWindowedSincPolyDataFilter to smooth surfaces without shrinkage.

I wonder if I can use the same filter to smooth curves without shrinkage too. The doc of the aforementioned filter states that it should be possible in principle. Also this paper by Taubin referred to both surface and line smoothing.
However, the following example segfaults.

import vtk
polygon = vtk.vtkRegularPolygonSource()
polygon.SetNumberOfSides(10)
polygon.GeneratePolylineOn() # No face
polygon.GeneratePolygonOff() # just polyline
polygon.Update()
polygon = polygon.GetOutput()
smoothed = vtk.vtkWindowedSincPolyDataFilter()
smoothed.SetInputData(polygon)
smoothed.SetNumberOfIterations(30)
smoothed.SetPassBand(0.3)
smoothed.SetBoundarySmoothing(False)
smoothed.SetNonManifoldSmoothing(False)
smoothed.SetNormalizeCoordinates(True)
smoothed.Update()

I address this question to @lassoan and @will.schroeder, because there has been recent development in vtkWindowedSincPolyDataFilter.

Thanks for your hints and clarifications :slight_smile:

Update. The segfault was present in vtk version 8.1. It seems fixed in version 9.0.

In version 9.0, however, no smoothing is applied at all for a polyline input, independent of the choice of parameters (iterations, passband, boundary smoothing, etc.).

The question remains: How could non-shrinking line smoothing be achieved?

2

Curve smoothing is quite different and it should be much simpler than surface smoothing, so I don’t think it should be added to surface smoothing filter.

For example, you can apply Fourier transform to the points, cut the number of coefficients and transform it back - about 10 lines of Python code. It would be nice if you could implement it in a proper VTK filter, as it would be easier to use, from both C++ and Python.

1 Like
3

Valuable input. Thanks!

Find below my attempt to smooth a polyline using FFT. I’m not an expert in signal processing, but it seems to work in the desired, non-shrinking way. Feedback is welcome.

from vtk.util.numpy_support import vtk_to_numpy, numpy_to_vtk
from scipy.fftpack import rfft, rfftfreq, irfft
# For newer versions of scipy, use:
# from scipy.fft import rfft, rfftfreq, irfft

def smoothedPolylineFFT(polyline, cutoff=0.5, closed=False):
    def _filter(y, cutoff):
        # Pretty much followed the instructions here.
        # https://realpython.com/python-scipy-fft/
        assert(0<=cutoff<=1)
        dt = 1/(len(y)-1)
        t = np.linspace(0,1,len(y))
        xf = rfftfreq(len(t), d=dt)
        yf = rfft(y)
        yf[int(cutoff*len(yf)):] = 0
        return irfft(yf)

    points = vtk_to_numpy(polyline.GetPoints().GetData())

    # Extend signal to avoid artifacts at beginning and end of the line.
    if closed:
        ns = points.shape[0]
        points = np.tile(points, (3, 1))
    else:
        ns = points.shape[0]//2
        points = np.concatenate([np.tile(points[0], (ns,1)),
                                 points,
                                 np.tile(points[-1], (ns,1))])
    points = np.apply_along_axis(_filter, axis=0, arr=points,
                                 cutoff=cutoff)
    # Undo signal extension
    points = points[ns:-ns+1]

    # Create new output poly.
    P = vtk.vtkPoints()
    P.SetData(numpy_to_vtk(points, deep=True))
    C = vtk.vtkCellArray()
    I = np.asarray([len(points)] + list(range(0,len(points))))
    C.SetCells(1, numpy_to_vtkIdTypeArray(I))
    result = vtk.vtkPolyData()
    result.SetPoints(P)
    result.SetLines(C)
    return result

For some polyline, I yield the following results:

p = createPolyLine()
q1 = smoothedPolylineFFT(p, cutoff=0.5, closed=True)
q2 = smoothedPolylineFFT(p, cutoff=0.3, closed=True)

image
image1664×1846 368 KB

By resampling the input line (e.g. equidistant piecewise-linear interpolation, not shown in the above sample code) the output can be further improved/smoothed. This requires to adjust the cutoff in the above script. But I believe there’s a functional relationship between normalized cutoff-frequency cutoff and the (re-)sampling rate, so that’s just fine.

2 Likes