Dear All,
Which the best way to remove displayed points of a volume, delimited by 6 planes?
I want to give 6x3 points (x,y,z each point) defining the planes and remove the points inside. Each plane defined by 3 points.
Thanks,
Luís Gonçalves
Hello, Luís,
Here is the code I use to remove points from an arbitrary hexahedron. Actually this code can be used for any polyhedron provided all faces are counter-clockwise when viewed from inside:
-------------------------vector3d.h-----------------------------
#ifndef VECTOR3D_H
#define VECTOR3D_H
class Vector3D {
public:
double x, y, z;
Vector3D operator-(Vector3D p) const;
Vector3D operator+(Vector3D p) const;
Vector3D cross(Vector3D p) const;
double dot(Vector3D p) const;
double norm() const;
};
Vector3D operator *( double scalar, const Vector3D& vector );
//make a point type with the same structure of the vector for clarity
typedef Vector3D Vertex3D;
#endif // VECTOR3D_H
---------------------------vector3d.cpp---------------------------------------------
#include "vector3d.h"
#include <cmath>
Vector3D Vector3D::operator-(Vector3D p) const {
return Vector3D{x - p.x, y - p.y, z - p.z};
}
Vector3D Vector3D::operator+(Vector3D p) const
{
return Vector3D{x + p.x, y + p.y, z + p.z};
}
Vector3D Vector3D::cross(Vector3D p) const {
return Vector3D{
y * p.z - p.y * z,
z * p.x - p.z * x,
x * p.y - p.x * y
};
}
double Vector3D::dot(Vector3D p) const {
return x * p.x + y * p.y + z * p.z;
}
double Vector3D::norm() const {
return std::sqrt(x*x + y*y + z*z);
}
Vector3D operator *(double scalar, const Vector3D & vector)
{
Vector3D result;
result.x = scalar * vector.x;
result.y = scalar * vector.y;
result.z = scalar * vector.z;
return result;
}
-------------------------face3d.h----------------------------
#ifndef FACE3D_H
#define FACE3D_H
#include "geometry/vector3d.h"
#include <vector>
class Face3D {
public:
Face3D(); //making the face with 4 vertexes by default
std::vector<Vertex3D> v;
Vector3D normal() const;
/** Computes the distance from point to the plane that contains this face. */
double distance( const Vertex3D& point ) const;
};
#endif // FACE3D_H
-----------------------face3d.cpp--------------------------------------
#include "face3d.h"
#include <cassert>
Face3D::Face3D() : v(4){}
// TODO: treat degenerate cases (e.g. a face may collapse into a triangle, edge or point).
// current GeoGrid constructors do not generate degenerate cells, but in the future, they might.
Vector3D Face3D::normal() const {
assert(v.size() > 2);
Vector3D dir1 = v[1] - v[0];
Vector3D dir2 = v[2] - v[0];
// dir1 cross dir2 or dir2 cross dir1 depends on whether the 3D coordinate system is right-handed or left-handed
Vector3D n = dir2.cross(dir1);
double d = n.norm();
return Vector3D{n.x / d, n.y / d, n.z / d};
}
double Face3D::distance(const Vertex3D & point) const
{
//Get the vector normal (n) to the plane of this face.
Vector3D n = normal();
//Plane of triangle:
// n . u = n . v[0], where u is any (x,y,z) contained in the plane (. == dot product).
// v[0] is a vertex of the face.
//Line that contains the point with direction given by the normal (n):
// u = point + tn (t is a scalar)
//Intersection point satisfies:
// n . ( point + tn ) = n . v[0]
// n . point + t = n . v[0]
double t = n.dot( v[0] ) - n.dot( point );
//Hence, the point that intersects the line and the plane, p0, is:
Vertex3D p0 = point + t * n;
//and the distance is point-to-p0 distance
return ( point - p0 ).norm();
}
--------------------------------THE METHOD----------------------------------------
/**
* This method assumes all faces are COUNTER-CLOCKWISE when viewed from INSIDE.
*
* Vertex id elements in the vId[8] array forming the geometry of a cell:
*
* J
* |
* |
*
* 3-----------2 face 0 = 0 1 2 3
* /| /| face 1 = 4 7 6 5
* / | / | face 2 = 0 3 7 4
* / | / | face 3 = 1 5 6 2
* 7--------- 6 | face 4 = 0 4 5 1
* | | | | face 5 = 3 2 6 7
* | 0----|------1 --- I
* | / | /
* | / | /
* |/ | /
* 4--------- 5
*
* /
* /
* K
*
*
*
*/
bool Util::isInside(const Vertex3D & p, const std::vector<Face3D> & fs)
{
double bound = -1e-15; // use -1e-15 to exclude boundaries
for (const Face3D& f : fs) {
Vector3D p2f = f.v[0] - p; // any point of f cloud be used
double d = p2f.dot( f.normal() );
d /= p2f.norm(); // for numeric stability
if ( d < bound )
return false;
}
return true;
}
I hope this helps.
abraço,
Paulo
Oops… Vertex3D = Vector3D: typedef Vector3D Vertex3D;
Thanks, for the code.
But I have similar code in C+CUDA for doing for unstructured images (Meshes) but for 6 random planes/faces (each with the information of the side of the plane to remove). For structured images (voxels) it is similar and easier.
What I want is if there is some filter in VTK to do something similar to a displayed image but in Python (VTK).
Off the top of my head, vtkExtractGeometry (which I believe takes an unstructured grid as input) should work. You have to provide it with a vtkImplicitFunction, in this case vtkPlanes. vtkPlanes must define a convex space. Also, each plane is defined by a point and a normal, so you’ll have to convert the three points into this form.
Complementing Will’s answer, you can get the normal vector from the three points defining the plane by using the cross product between two non-parallel vectors. Chose one point as the common origin of the two vectors. Each vector is then defined by this common origin and another point.
In the code I provided above, the method Vector3D::cross() can be used to compute the normal (translating it to Python should be easy). Again, ordering is important here too:
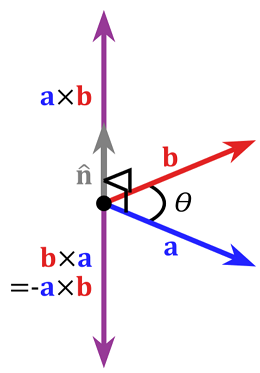
Tanks, Will.
Dear All,
Can somebody advise me?
I have 6 planes defined by 3 points each. And a 4th point defining the side of the plane I want to select.
I do the cross product to find the normal to the plane. I do the dot product between the (4th point minus onepointofplane) and the normal of the plane to find the right direction of the normal.
I want to remove the polygon volume defined by those 6 planes from a preexistent volume (self.volume). For that I delete self.volume and create a new one supposed without the polygon volume. I used self.reader.GetOutputPort() that contains the original image. I have stability errors e.g system instability. Perhaps problems with OpenGL.
Need I to delete the original volume? There is a better way to delete the polygon volume in the original image directly? What the errors below?
plane1 = vtk.vtkPlane()
plane1.SetOrigin(self.x1[0],self.y1[0],self.z1[0])
p3p1=np.array([self.x1[2]-self.x1[0],self.y1[2]-self.y1[0],self.z1[2]-self.z1[0]])
p2p1=np.array([self.x1[1]-self.x1[0],self.y1[1]-self.y1[0],self.z1[1]-self.z1[0]])
cross1=np.cross(p3p1,p2p1)
cross1=cross1/np.linalg.norm(cross1)
dot1=cross1[0]*(self.sidex[0]-self.x1[0])+cross1[1]*(self.sidey[0]-self.y1[0])+cross1[2]*(self.sidez[0]-self.z1[0])
if (dot1 < 0.0):
cross1=-cross1
plane1.SetNormal(cross1[0],cross1[1],cross1[2])
code for plane2 to plane6
union = vtk.vtkImplicitBoolean()
union.AddFunction(plane1)
union.AddFunction(plane2)
union.AddFunction(plane3)
union.AddFunction(plane4)
union.AddFunction(plane5)
union.AddFunction(plane6)
union.SetOperationType(0) #union
extract = vtk.vtkExtractGeometry()
extract.SetInputConnection(self.reader.GetOutputPort())
extract.SetImplicitFunction(union)
volumeMapper = vtk.vtkOpenGLGPUVolumeRayCastMapper()
volumeMapper.SetInputConnection(extract.GetOutputPort())
volumeColor = vtk.vtkColorTransferFunction()
volumeColor.AddRGBPoint(0,0.0,0.0,0.0)
volumeColor.AddRGBPoint(255,0.0,0.0,1.0)
volumeScalarOpacity = vtk.vtkPiecewiseFunction()
volumeScalarOpacity.AddPoint(0,0.0)
volumeScalarOpacity.AddPoint(255,1.0)
volumeGradientOpacity = vtk.vtkPiecewiseFunction()
volumeGradientOpacity.AddPoint(0,1.0)
volumeGradientOpacity.AddPoint(255,1.0)
volumeProperty = vtk.vtkVolumeProperty()
volumeProperty.SetColor(volumeColor)
volumeProperty.SetScalarOpacity(volumeScalarOpacity)
volumeProperty.SetGradientOpacity(volumeGradientOpacity)
volumeProperty.SetInterpolationTypeToLinear()
volumeProperty.ShadeOff()
volumeProperty.SetAmbient(0.6)
volumeProperty.SetDiffuse(0.6)
volumeProperty.SetSpecular(0.1)
renderer.RemoveVolume(self.volume)
renderWindow.Render()
self.volume = vtk.vtkVolume()
self.volume.SetMapper(volumeMapper)
self.volume.SetProperty(volumeProperty)
renderer.AddVolume(self.volume)
renderWindow.Render()
Thanks,
Luís Gonçalves