Shortest path with vtkDijkstraGraphGeodesicPath

Support
1

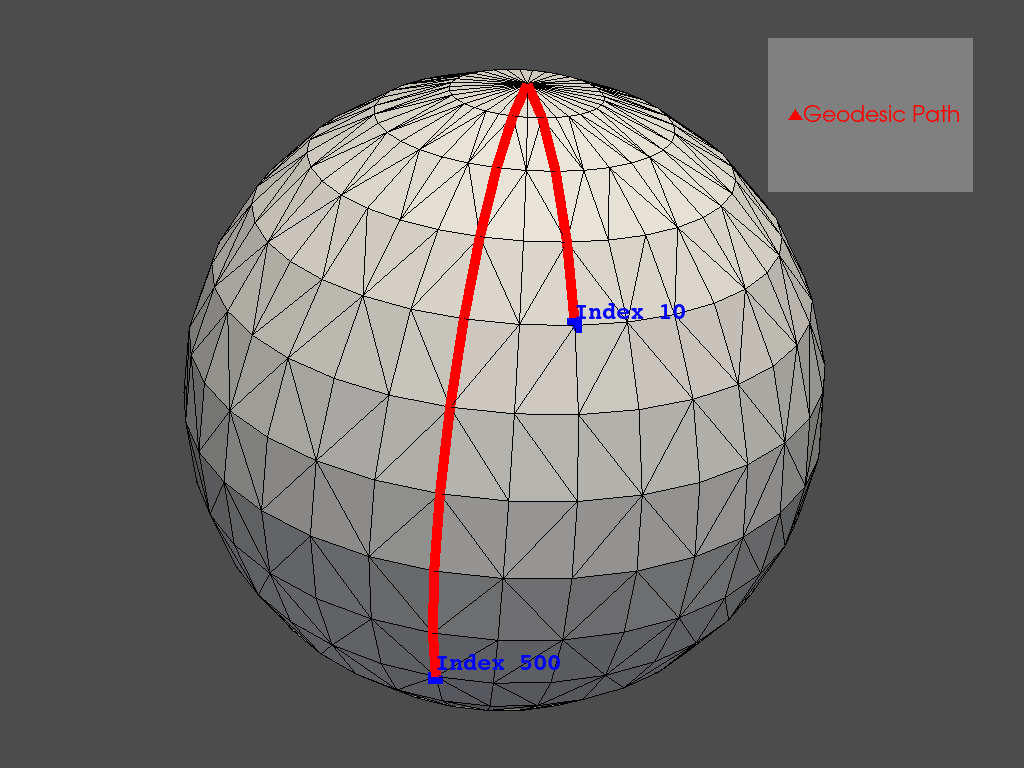
Over in PyVista, we’re running into a slight bug when using the vtkDijkstraGraphGeodesicPath algorithm to calculate the geodesic path between two vertices on a surface mesh. When playing around with the algorithm, I happened to choose vertices on this particular mesh that the vtkDijkstraGraphGeodesicPath appears to not be able to find the shortest path.

Load this example file: globe.vtk (45.1 KB)

Then try to find the path between nodes 10 and 500.

Please note that I am using PyVista to perform the file IO and plotting as I want to focus this discussion on the usage of the vtkDijkstraGraphGeodesicPath algorithm.

import vtk
import pyvista as pv

# read the mesh
sphere = pv.read('globe.vtk')

# Run the Dijkstra algorithm
dijkstra = vtk.vtkDijkstraGraphGeodesicPath()
dijkstra.SetInputData(sphere)
dijkstra.SetStartVertex(10)
dijkstra.SetEndVertex(500)
dijkstra.Update()

geodesic = pv.wrap(dijkstra.GetOutput())

And now plot it in comparison to the edges of the input mesh:

p = pv.Plotter()
p.add_mesh(geodesic, line_width=10, color='red', label='Geodesic Path')
p.add_mesh(sphere, show_edges=True, color=True)
p.add_point_labels(sphere.points[[10, 500]], ['Index 10', 'Index 500'], 
                   point_size=15, color='blue', font_size=24)
# View the path
p.camera_position = [(-24874896399.14252, 5320221544.881892, 14139125256.713934),
                     (21057021.541644454, -143014260.7912798, 115865941.12124935),
                     (0.48576786647743864, -0.02878481343390217, 0.8736137672985315)]
p.add_legend()
p.show()

download
download.png1024×768 47.3 KB

Any help on figuring out why this particular example isn’t resulting in the shortest path would be greatly appreciated!

2

I’m on my phone so can’t look at your globe object, but I suspect that the sphere is split on the meridian most directly facing the camera. That is, there are duplicate points along that meridian so that the shortest path cannot cross where visually it looks like it should. That would explain the detour to the pole.

3

Ahhh, of course! It is split there :man_facepalming: