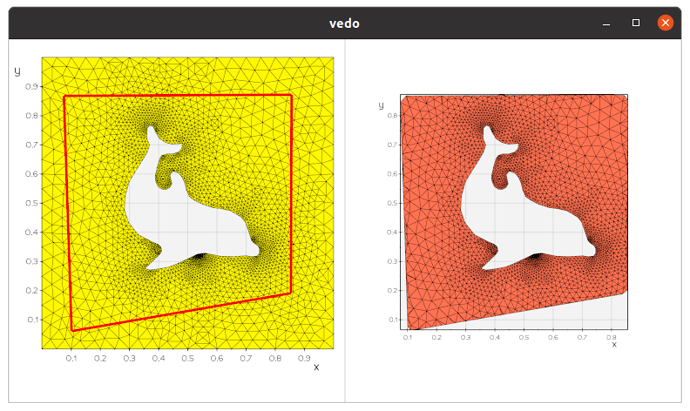
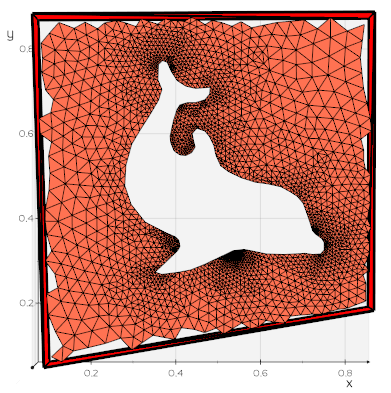
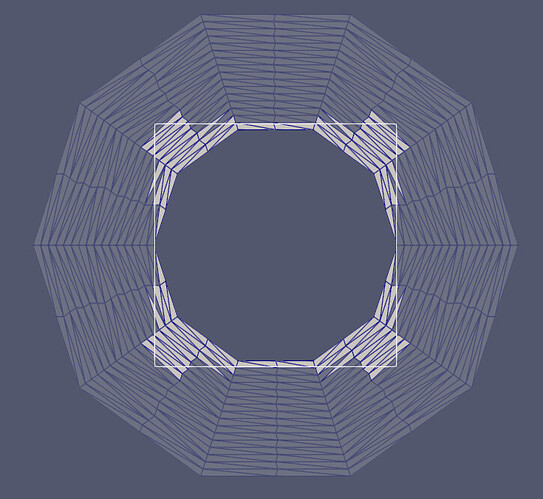
Thanks for the responses, and for introducing me to some new VTK filters and vedo!
I am a bit hesitant to use clipping with an implicit function due to the discussion in https://www.vtkjournal.org/browse/publication/797.
I did find a solution using vtkIntersectionPolyDataFilter with the following approach:
- Create a polyline from the points
- Extrude the polyline to form a skirt which intersects the surface (if the points originally lie exactly on the surface, then you only need to extrude by some small epsilon)
- Intersect the original surface with vtkIntersectionPolyDataFilter. This returns the intersection polyline, and the two surfaces which are remeshed to form triangular cells from the split cells.
The example below (uses pyvista) adds the edges of a trapezoid projected onto a sphere.
import pyvista as pv
import vtk
surf = pv.Sphere(center=(0, 0, 0), radius=200)
polyline = pv.PolyLine([(10, 0, 0),
(10, 50, 0),
(10, 25, 100),
(10, 0, 100)], closed=True)
skirt = polyline.extrude((400, 0, 0)).triangulate().clean().extract_surface()
f = vtk.vtkIntersectionPolyDataFilter()
f.SetInputDataObject(0, surf)
f.SetInputDataObject(1, skirt)
f.SetComputeIntersectionPointArray(True)
f.Update()
intersection_polyline = pv.wrap(f.GetOutputDataObject(0)) # intersection of the two surfaces
surf_remeshed = pv.wrap(f.GetOutputDataObject(1)) # the surface which has been remeshed along the split
skirt_remeshed = pv.wrap(f.GetOutputDataObject(2)) # the skirt which has been remeshed along the split
p = pv.Plotter(shape=(1, 2))
p.subplot(0, 0)
p.add_mesh(surf, style='wireframe', color='g')
p.add_mesh(surf.copy(), opacity=0.5, color='g')
p.add_mesh(skirt, style='wireframe', color='b')
p.add_mesh(skirt.copy(), opacity=0.5, color='b')
p.subplot(0, 1)
p.add_mesh(surf_remeshed, style='wireframe')
p.add_mesh(surf_remeshed.copy(), opacity=1.0, color='g')
p.link_views()
p.show()
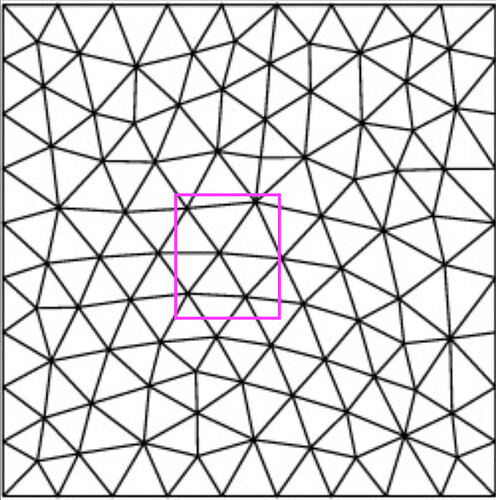
 . I could be way off, but I feel like a lot of the machinery already exists in either vtkClipPolyData or vtkBooleanOperationPolyDataFilter.
. I could be way off, but I feel like a lot of the machinery already exists in either vtkClipPolyData or vtkBooleanOperationPolyDataFilter.