It appears that one can set either the vertical or horizontal visual angles of a camera. If I was to set either of these (say the horizontal visual angle range) how would I find what is the other visual range (in this case the vertical one)?
Hello,
What do you mean by “angular ranges”? Do you mean camera altitude and azimuth (where it points) or the field of view angles (pan/wide/narrow view)?
regards,
Paulo
Hi Paulo,
Here I was referring to the the field of view . So for instance, the horizontal range (115 for binocular) and 135 deg in horizontal and say 100 for the vertical range.
thanks,
M
Hello,
vtkCamera has the setViewAngle(double) method which sets the field-of-view angle (30º by default, ignored if projection is set to parallel). It is not possible to set two angles with that method. To achieve that (you’ll end up with distorted aspect ratio, I must warn you) you have to call UseExplicitProjectionTransformMatrixOn() and set the projection matrix manually. Please, take a look at this (c++ - What is the difference between ProjectionTransformMatrix of VTK and GL_PROJECTION of OpenGL? - Stack Overflow) to get started with setting projection matrices. Even though, you can’t set the vert/horiz angles directly. You have to express them as vert/horiz and horiz/vert ratios. In the figures below, you have a typical viewing frustum used in perspective projection and how the parameters relate to elements in the projection matrix further below.
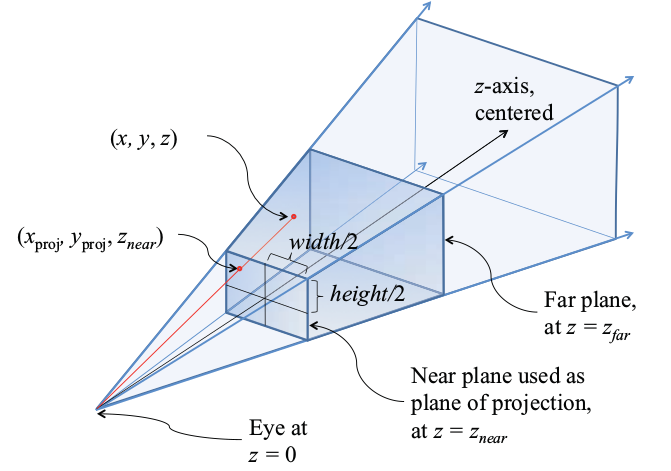

figures taken from: OpenGL “Red Book”.
take care,
Paulo
Thank you Paulo.
Just a quick follow up. So from what you say I’d gather that by knowing any of the visual angles (whether the vertical or the horizontal) and dividing by the size (in pixels) of the window, we should be able to determine what is the angle subtended by each pixel. Correct?
I’d say that your rationale is accurate for the “pixels” of our retina, which is a spherical sensor. However, that is not accurately valid when we talk about planes. If you imagine the pixels farthest from the screen center, they will cover lower angles (see figure below). But your calculation is an estimate good enough provided the field of view angle is not too large. The angular size of the pixel right in front of the camera is maximum and decreases asymptotically with the distance from the center, more or less like a Gaussian curve with a large sigma.
Thank you Paulo! Indeed, my thinking was based on a previous model I had worked on which used a spherical projection. Thanks for the clarification!