vtkCurvatures yields unreasonably large values along borders

Support
1

Hi

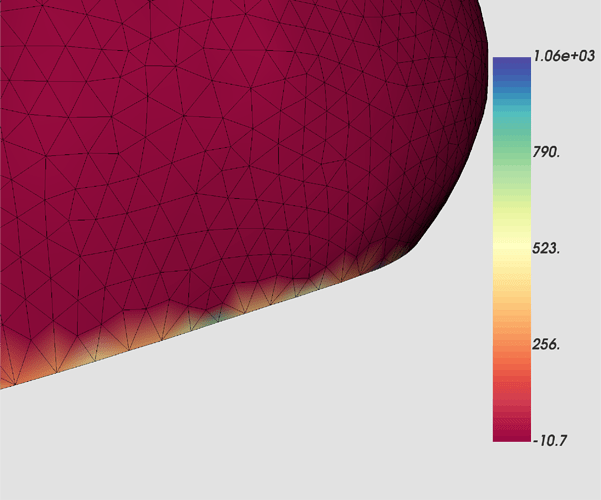
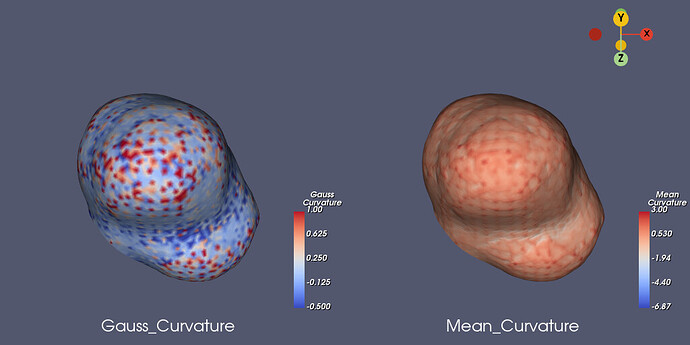
Does anyone know why vtkCurvatures yields unreasonably high values close to the object’s border? See screenshot below. I expect the (Gaussian) curvature for my shapes to be in the range [-0.5,1]. However, I observe values along the border that are several orders of magnitude larger/smaller.

Does anyone have experience how to deal with this?

image
image2510×2088 860 KB

Here is how to reproduce the problem:

curvature = vtk.vtkCurvatures()
curvature.SetInputConnection(source.GetOutputPort())
curvature.SetCurvatureTypeToGaussian()
curvature.Update()

I also attached a sample geometry:
curvature.vtp (237.4 KB)

1 Like
2

It is possible that your mesh have some tiny faces, degenerate faces or duplicate vertexes. Can you try vtkCleanPolyData to rule out that possibility?

3

I verified this. My surface is clean. This seems not to be the problem.

4

You may like to look at CurvatureBandsWithGlyphs. In this example, the random hills surface will generate large irregular values for curvatures along the edges, so the surface is clipped. Curvatures along edges will most likely yield erroneous values so clipping would be appropriate after generating the curvatures.

2 Likes
5

Check out definition of discrete Gaussian curvature. For me, it seems that the formula that vtkCurvatures uses in Gaussian mode is correct for internal vertices but incorrect for edge vertices.

A simple solution is what is suggested above: ignore curvature of edge vertices.

A nicer solution would be compute curvature of edge vertices by averaging curvature of nearby internal vertices.

1 Like
6

@lassoan you are correct in that the formula is correct for internal vertices. Way back in 2002 I think that we did consider points on an edge but even averaging yielded strange values so nothing more was done. The formula is correct for closed orientable surfaces. For edges and holes, clipping would be the best approach after calculating the curvatures.

7

Copying value from closest non-boundary neighbor (or weighted average of non-boundary neighbors) should work, but even just setting boundary voxels curvature to 0 would be better than setting incorrect values.

8

Thanks you Andras and Andrew for your useful answers.

@lassoan That was a good read. In particular, I liked the geometric interpretation of Mean and Gaussian curvature. Based on those slides, I conclude that the problem is present only for Gaussian curvature, but not for Mean curvature, right? What I don’t get is why the curvature peaks are so large (100-1000 than usually), and why Gaussian curvature is computed at all if it is not defined along the surface boundary.

@amaclean Regarding clipping: I mentioned that I expect the values to be in a certain range for the sample geometry I provided, but I’m not entirely sure how this generalizes to other objects. With clipping, one has to make a somewhat arbitrary choice of the clipping thresholds. I don’t feel very comfortable with it. I considered to apply outlier detection (for example based on robust z-scores), which would we feasible for the type of surfaces I deal with: smooth “organic” structures, with a half-sphere as basic shape from which nature deviated gradually.

9

What I finally did: Since Gaussian curvature is not defined along the surface boundary, I decided to remove those values using a weighted averaging, just as Andras suggested. For my purpose, this is better than setting the curvature to 0.

    def computeGaussCurvatureAndFixUpBoundary(source):
        # Curvature as vtkPolyData.
        source = source.GetOutput() # source: vtkPolyData
        curvatureData, arrayName = computeCurvature(source)
        # Curvature as python list.
        curvature = extractData(curvatureData, arrayName)
        # Ids of the boundary points.
        pIds = extractEdgeIds(source) 
        pIdsSet = set(pIds)

        # Iterate the edge points and compute the curvature as the weighted
        # average of the neighbors.
        countInvalid = 0
        for pId in pIds:
            pIdsNeighbors = pointNeighborhood(source=source, pId=pId)
            # Keep only interior points.
            pIdsNeighbors -= pIdsSet
            # Compute distances and extract curvature values.
            curvs = [curvature[pIdN] for pIdN in pIdsNeighbors]
            dists = [computeDistance(source, pIdN, pId) for pIdN in pIdsNeighbors]
            curvs = np.array(curvs)
            dists = np.array(dists)
            curvs = curvs[dists>0]
            dists = dists[dists>0]
            if len(curvs)>0:
                weights = 1/np.array(dists)
                weights /= weights.sum()
                newCurv = np.dot(curvs, weights)
            else:
                # Corner case.
                countInvalid += 1
                newCurv = 0
            # Set new curvature value.
            curvature[pId] = newCurv
        return curvature

Here, some details about the utilities I used in the above code.

    def computeCurvature(source):
        curvatureFilter = vtk.vtkCurvatures()
        curvatureFilter.SetInputData(source)
        curvatureFilter.SetCurvatureTypeToGaussian()
        arrayName = "Gauss_Curvature"
        curvatureFilter.Update()
        return curvatureFilter.GetOutput(), arrayName

    def extractEdgeIds(source):
        """
        See here: https://discourse.vtk.org/t/2530/3
        """
        ...

    def extractData(source, arrayName):
        array = source.GetPointData().GetArray(arrayName)
        n = source.GetNumberOfPoints()
        data = []
        for i in range(n):
            data.append(array.GetValue(i))
        return data

    def pointNeighborhood(source, pId):
        """
        Extract the topological neighbors for point pId. In two steps:
        1) source.GetPointCells(pId, cellIds)
        2) source.GetCellPoints(cId, pointIds) for all cId in cellIds
        """
        ...

    def computeDistance(source, pIdA, pIdB):
        pA = np.array(source.GetPoint(pIdA))
        pB = np.array(source.GetPoint(pIdB))
        return np.linalg.norm(pA-pB)
3 Likes
10

@normanius Based on the comments here, I have created a class that generates the Gaussian and Mean curvatures, adjusting curvature for edge variations.

Please see: CurvaturesAdjustEdges for Python and CurvaturesAdjustEdges for C++.

If you run the Python example with your data as follows:

    reader = vtk.vtkXMLPolyDataReader()
    reader.SetFileName('./curvature.vtp')
    reader.Update()
    source = reader.GetOutput()

    cc = ComputeCurvatures(source)
    cc.set_gauss_curvature_bounds(-0.5, 1.0)
    cc.gauss_bounds_on()

    cc.update()

    # Uncomment the following lines if you want to write out the polydata.
    writer = vtk.vtkXMLPolyDataWriter()
    writer.SetFileName('Source.vtp')
    writer.SetInputData(source)
    writer.SetDataModeToAscii()
    writer.Write()

I get this result:

curvature
curvature1024×512 61.8 KB

1 Like
11

What are the color scales of both figures?

12

Here are the bands with ranges and frequencies. I have just split the data into 10 bins so you can see the distribution.

Gaussian Curvature:

    cc = ComputeCurvatures(source)
    cc.set_gauss_curvature_bounds(-0.5, 1.0)
    cc.gauss_bounds_on()

Bands & frequencies:
   0 [  -0.500,   -0.425,   -0.350]:    290
   1 [  -0.350,   -0.275,   -0.200]:    208
   2 [  -0.200,   -0.125,   -0.050]:    358
   3 [  -0.050,    0.025,    0.100]:    684
   4 [   0.100,    0.175,    0.250]:    829
   5 [   0.250,    0.325,    0.400]:    769
   6 [   0.400,    0.475,    0.550]:    610
   7 [   0.550,    0.625,    0.700]:    501
   8 [   0.700,    0.775,    0.850]:    372
   9 [   0.850,    0.925,    1.000]:    247

Mean Curvature:

No bounds set for the mean curvature so all the adjusted curvatures are used.

Bands & frequencies:
   0 [  -6.868,   -6.375,   -5.881]:      1
   1 [  -5.881,   -5.388,   -4.895]:      2
   2 [  -4.895,   -4.402,   -3.909]:      1
   3 [  -3.909,   -3.416,   -2.923]:      3
   4 [  -2.923,   -2.429,   -1.936]:     11
   5 [  -1.936,   -1.443,   -0.950]:     44
   6 [  -0.950,   -0.457,    0.036]:   1141
   7 [   0.036,    0.530,    1.023]:   3699
   8 [   1.023,    1.516,    2.009]:    436
   9 [   2.009,    2.502,    2.995]:     19
13

Let me rephrase the question: can you post the same figure with color scale bars?

14

This is great! Could you add this cleanup to vtkCurvatures filter? It could be enabled/disabled with a flag for performance and backward compatibility reasons.

15

That is a good idea (it will make my life simpler)! I’ll add it to vtkCurvatures.

16

Done, I have also updated CurvaturesAdjustEdges and
CurvaturesDemo

CurvaturesAdjustEdges
CurvaturesAdjustEdges1024×512 71 KB

1 Like